Do you wanna win?

Song: The Impressions, "Do You Wanna Win?"

(This is an excerpt from a larger project about sports gambling. Code used, and early drafts of some of the chapters can be found at https://github.com/csdurfee/book.)

I'm going to return to the subject of sports betting this week. Let's start with something easy. How do you avoid going broke betting on sports? That's easy. Reduce your bet size to zero. Scared money don't lose none.

As long as there is randomness, there will be outliers and unexpected results. It is impossible to escape randomness in sports betting. Any time you decide to bet, you enter the kingdom of randomness and have to abide by its laws. It doesn't matter whether you have an advantage over the house (unless the advantage is truly massive). Nothing is guaranteed.

This is a pretty hard thing for us to know how to deal with, when our brains are pattern-finding machines. Our brains will find patterns to give us a sense of control.

Notes

I talk about "win rate" a bunch below. That means the percent of the time a gambler can win bets at even odds (such as a standard spread bet on the NBA or NFL.)

The random walks shown below are a little different from a standard one, because I'm simulating the vig. The walker goes 1 block north when the coin comes up heads (or they win the bet), and 1.1 blocks south when the coin comes up tails (or they lose the bet.)

In the marches of madness

The NCAA holds the March Madness tournament every year to determine who the best college basketball team is. It's a single elimination tournament of 64 teams, arranged into a big bracket.

Say we do a March Madness style bracket with coin flippers instead of basketball teams. We randomly assign them places in the bracket. For each matchup, the coin flipper at the top of the matchup flips a coin. If they get heads, they survive and advance. If they get tails, they lose.

Somebody's going to go 6-0 and win that tournament.

Now imagine we expanded that to every single person on the planet. Every single person gets matched up into a 64 person bracket, then each of those winners get added to another 64 team bracket, and so on.

Eventually, someone has to emerge the victor with a 32-0 record or something -- the greatest coin flipper in the world. Right?

Random walks

Imagine going on a walk. Every time you get to an intersection, you flip a coin. If it's heads, you go one block north and one block east. If it's tails, you go one block south and one block east. This is called a random walk. It's a bit like a gambler's profits or losses plotted on a graph as a function of time.

I think there's a huge value in knowing what random walks look like. Do they remind you of anything?

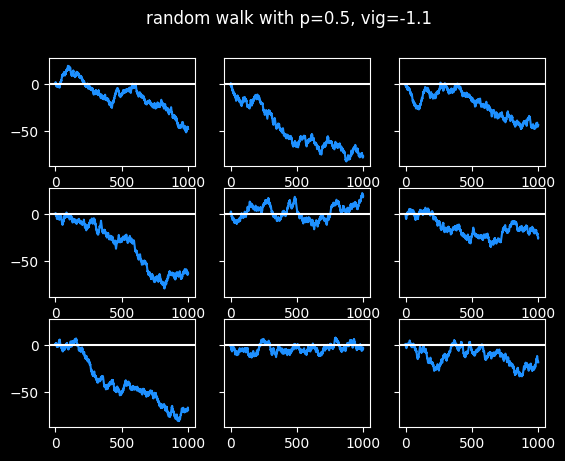
Touts are people who sell recommendations about which bets to take. Pay $30 and they'll tell you which side to bet on the big game tonight. (I have a whole section about touts in the book.) The best tout I could find has had pretty steady success for nearly 20 years, with a win rate of 54.1% against the standard vig. That's statistically significant, but it's not enough to guarantee success moving forwards. Let's look at some random walks at 54.1% win rate:

Most of them ended up +25-50 units after 1000 bets, which is pretty good. But a couple of them ended up being losers, even with the advantage. The touts I looked at generally don't sell picks for every single game. So with 1200 games in an NBA season, this could be several years' worth of results.

Imagine all of these as 9 different touts, with the exact same level of skill at picking games. But some of them look like geniuses, and some look like bozos. There would probably be some selection bias. The ones with the bad records would drop out -- who's buying their picks if they're losing money? And the ones who did better than their true skill level of 54.1% would be more likely to stick with it. Yet all these random walks were generated with the same 54.1% win rate.

If you bought 1,000 picks from this tout, you don't get to choose which of the \(2^{1000} = (2^{10})^{100} \approx 10^{300}\) possible random walks you will actually get. If each bet has a 54.1% chance of winning, there's no guarantee you will have exactly 541 wins and 459 losses at the end of 1000 bets.

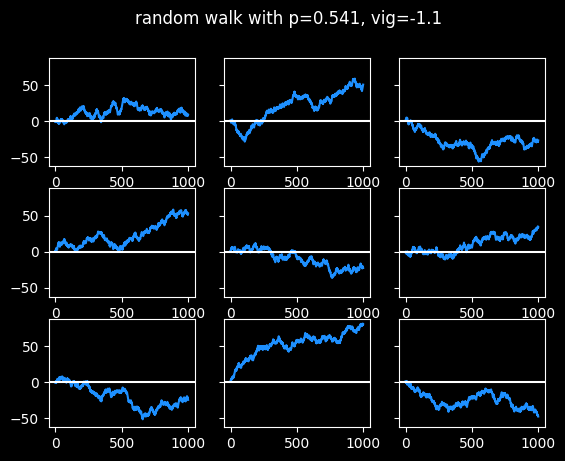
Here's what someone who is right 60% of the time looks like.

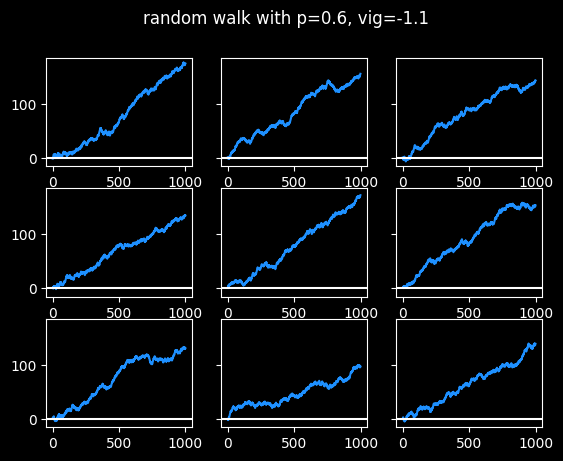
Success is pretty boring.

I've always said it's much harder to learn from success than from failure. At a 60% win rate, none of them really have long cold streaks, just small breaks between hot streaks. It wouldn't be interesting to tell stories about those graphs. There's nothing to learn, really.

I don't think it's possible to win 60% against the spread, for reasons discussed in the book. The short version is we can convert a gambler's win rate to points on the spread. Even people who do have an advantage over the house are probably going to be closer to that 54.1% mark.

The graphs at the 54.1% success rate appear a lot more human. They have hot and cold streaks, swoons, periods where they seem stuck in a range of values. Some of them scuffled the whole time, a couple finally got locked in near the end, a couple were consistently good. Some had good years, some had bad years. Even though they are randomly generated, they look like they have more to teach us, like they offer more opportunities to tell stories. But they all have the exact same win rate, or level of skill at handicapping.

No outcome is guaranteed, but the higher the win rate, the more consistently the graph is going to go up and to the right at a steady pace.

Finally, here are some walks at 52.4% win rate, the break-even point. Most results end up close to zero after 1000 bets, but there is always a possibility of an extended run towards the positive or negative side (4/9 times in this sample).

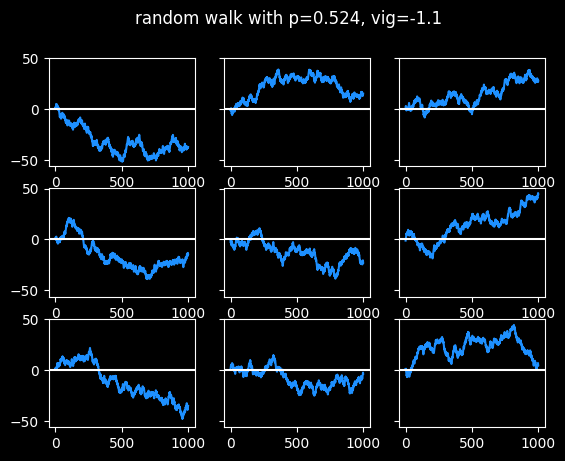
The Axe Forgets, The Tree Remembers

If those 9 graphs were stock prices, which one would you consider the best investment?

Well, we know they're equally bad investments. They're winning just enough to break even, but not make profits.

They all have the same Expected Value moving forwards. Previous results are meaningless and have no bearing on whether the next step will be up or down. Every step is the start of an entirely new random walk. The coin doesn't remember what has happened in the past. We do.

This is what's known in math as a Martingale, named after a betting system that was popular in France hundreds of years ago. (I previously talked about Martingales in the series on the hot hand.)

The basic idea behind all these betting systems is to chase losses by betting more when you're losing. Hopefully it's obvious that these chase systems are crazy, though formally proving it led to a lot of interesting math.

Fallacy and ruin

Even though chase systems are crazy, they've persisted through the centuries. Human beings are wired to be semi-rational -- we use previous data to try and predict the future, but we use it even when the data was randomly generated, and even when we don't have a significant amount of data. We need coherent stories to tell about why things happened. There is no rational reason to believe in a chase system, but I think there are semi-rational reasons to fall prey to the gambler's fallacy.

I hope these random walks show that having a modest, plausible advantage over the house isn't a guarantee of success, even over a really long timespan. Positive Expected Value is necessary, but not sufficient, for making money long term.

The vast majority of gamblers bet with negative expected value due to the vig, and possibly biases in the lines, as we saw in a previous installment. If each bet the average gambler makes has a negative expected value, they can't fix that by betting MORE.

"If I keep doubling down, eventually I'll win it all back." Maybe if you have infinite capital and unlimited time. Otherwise the Gambler's Ruin is certain. The market can stay liquid longer than you can stay irrational.

Maximizing profits: the Kelly criterion

Let's say a bettor really does have an edge over the house -- they can beat the spreads on NBA basketball 56% of the time.

Even with that advantage, it's easy to go broke betting too much at once. Suppose they bet 25% of their bankroll on each bet. What happens after 200 bets? 200 bets is not a lot, roughly 1 month of NBA games if they bet on every game.

Once in a blue moon they end up a big winner, but 53% of the time the gambler is left with less than 5% of their bankroll after 200 bets even though they have a pretty healthy advantage over the house. So it's still a game of chance rather than skill, even though it would require a lot of mental labor to make the picks, and time to actually bet the picks. The mean rate of return is quite impressive (turning $100 into $4,650), but the median result is bankruptcy (turning $100 into $3).

Intuitively, there has to be some connection between the betting advantage and the optimal amount to risk on each bet. If a gambler only has a tiny advantage, they should only be making tiny bets as a percentage of their total bankroll. The better they are, the more they can risk. And if they have no advantage, they shouldn't bet real money at all.

That intuition is correct. The Kelly criterion gives a formula for the exact percent of the bankroll to risk on each bet in order to maximize Expected Value, given a certain level of advantage. https://en.wikipedia.org/wiki/Kelly_criterion

In this case, the Kelly criterion says to bet 7.6% of the total bankroll on each bet. I did 100,000 simulations of a sequence of 200 bets following the Kelly criterion. The gambler only went broke around one time in 1,000, which is much better. The median result was turning $100 into $168, which is pretty good. However, the gambler still lost money 31% of the time.

This is just one month of betting, assuming the gambler bets on every NBA game. Losing money 31% of the time seems pretty high for what's supposed to be the optimal way to bet.

How about a longer period of time? I simulated 1,000 bets this time, nearly a whole season of the NBA. The median outcome is turning $100 into $1356, which is a sweet rate of return. But the chances of going broke actually increased! The player will go broke 1.4% of the time, about 11x more often on 1000 bets than 200, which seems unfair, but the Kelly criterion doesn't make any guarantees about not going broke. It just offers the way to optimize Expected Value if the gambler knows the exact advantage they have over the house.

Partial Kelly Betting

Kelly Betting is the optimal way to maximize profits, but what about lower stakes? The real power of Kelly betting is its compounding nature -- as the bankroll gets bigger or smaller, the bet size scales up or down as well.

What if the gambler only bets 2% of their bankroll instead of the 7.6% recommended by the Kelly criterion? They don't go broke a single time in 100,000 simulations of 1,000 bets. The mean rate of return is 4.6x and the median is 3.7x. That's a pretty nice return on investment, relative to the risk. The gambler still lost money 2.8% of the time, though. Being conservative, betting a lot of games at positive expected value, and betting the right way greatly increase the chances of success, but nothing can eliminate the possibility of failure.

Imagine doing 1000 bets at 56% win percentage and a conservative bet size, and still losing money. Wild, isn't it? If you take one thing away from this article, it should be:

Failure is always an option.

Betting a constant amount

You wouldn't have that problem with betting a constant amount, right? Say a gambler has a bankroll of $100 and bets to win $20 on each game. 1000 games, 56 win %.

This Expected Value of playing this way doesn't have any randomness in it. It's just a simple algebra problem. According to EV, they should end up with $252 at the end of the season, for a profit of $152. Nice. But as I've mentioned before, EV says nothing about the range of possible outcomes.

If I actually simulate it, a pretty wide range of outcomes are possible. 99% of the time, the gambler makes money, but 6 times out of 100,000, they lose everything and more. (6 in 100,000 is about the same odds as winning a 14 leg parlay.)

With betting a fixed size, the rate of return is lower and the risk of going broke doesn't go away. So it's sub-optimal compared to Kelly-style betting with a very small percentage of the total bankroll.

Next time

More on random walks... probably.