One in e
Song: Klonhertz, "Three Girl Rhumba"
Notebook available here
Think of a number
Pick a number between 1-100.
Say I write down the numbers from 1-100 on pieces of paper and put them in a big bag, and randomly select from them. After every selection, I put the paper back in the bag, so the same number can get picked more than once. If I do that 100 times, what is the chance of your number being chosen?
The math isn't too tricky. It's often easier to calculate the chances of a thing not happening, then subtract that from 1, to get the chances of the thing happening. There's a 99/100 chance your number doesn't get picked each time. So the probability of never getting selected is \((99/100)^{100} = .366\). Subtract that from one, and there's a 63.4% chance your number will be chosen. Alternately, we'd expect to get 634 unique numbers in 1000 selections.
When I start picking numbers, there's a low chance of getting a duplicate, but that increases as I go along. On my second pick, there's only a 1/100 chance of getting a duplicate. But if I'm near the end and have gotten 60 uniques so far, there's a 60/100 chance.
It's kind of a self-correcting process. Every time I pick a unique number, it increases the odds of getting a duplicate on the next pick. Each pick is independent, but the likelihood of getting a duplicate is not.
I could choose the numbers by flipping a biased coin that comes up heads 63.4% of the time for each one instead. I will get the same number of values on average, and they will be randomly chosen, but the count of values will be much more variable:
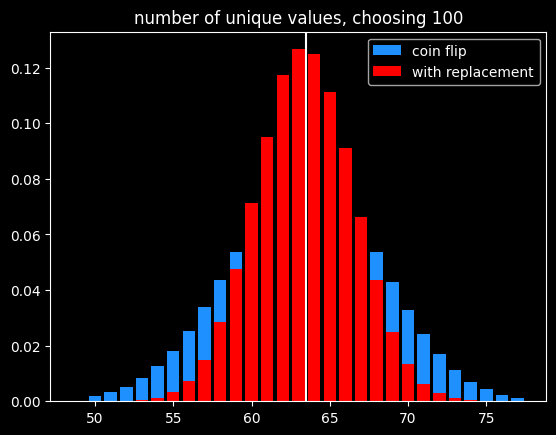
Of course, if the goal is to select exactly 63 items out of 100, the best way would be to randomly select 63 without replacement so there is no variation in the number of items selected.
A number's a number
Instead of selecting 100 times from 100 numbers, what if we selected a bajillion times from a bajillion numbers? To put it in math terms, what is \(\lim\limits_{n\to\infty} (\frac{n-1}{n})^{n}\) ?
It turns out this is equal to \(\frac{1}{e}\) ! Yeah, e! Your old buddy from calculus class. You know, the \(e^{i\pi}\) guy?
As n goes to infinity, the probability of a number being selected is \(1-\frac{1}{e} = .632\). This leads to a technique called bootstrapping, or ".632 selection" in machine learning (back to that in a minute).
Don't think of an answer
What are the chances that a number gets selected exactly once? Turns out, it's \(\frac{1}{e}\), same as the chances of not getting selected! This was surprising enough to me to bother to work out the proof, given at the end.
That means the chances of a number getting selected more than once is \(1 - \frac{2}{e}\).
The breakdown:
- 1/e (36.8%) of numbers don't get selected
- 1/e (36.8%) get selected exactly once
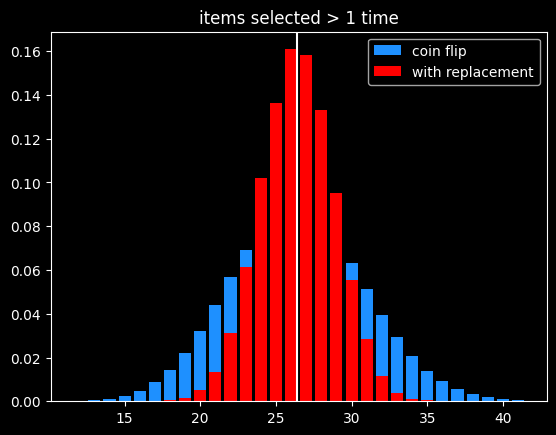
- 1-2/e (26.4%) get selected 2+ times
As before, the variance in number of items picked 2+ times is much lower than flipping a coin that comes up heads 26.4% of the time:
Derangements
Say I'm handing out coats randomly after a party. What are the chances that nobody gets their own coat back?
This is called a derangement, and the probability is also 1/e. An almost correct way to think about this is the chance of each person not getting their own coat (or each coat not getting their own person, depending on your perspective) is \(\frac{(x-1)}{x}\) and there are \(x\) coats, so the chances of a derangement are \(\frac{x-1}{x}^{x}\).
This is wrong because each round isn't independent. In the first case, we were doing selection with replacement, so a number being picked one round doesn't affect its probability of being picked next round. That's not the case here. Say we've got the numbers 1 thru 4. To make a derangement, the first selection can be 2, 3 or 4. The second selection can be 1, 3 or 4. But 3 or 4 might have been picked in the first selection and can't be chosen again. 2/3rds of the time, there will only be two options for the second selection, not three.
The long way 'round the mountain involves introducing a new mathematical function called the subfactorial, denoted as \(!x\), which is equal to the integer closest to \(\frac{x!}{e}\). \(e\) gets in there because in the course of counting the number of possible derangements, a series is produced that converges to \(1/e\).
The number of derangements for a set of size x is \(!x\) and the number of permutations is \(x!\), so the probability of a derangement as x gets big is \(\frac{!x}{x!} = \frac{1}{e}\)
What about the chances of only one person getting their coat back? It's also \(\frac{1}{e}\), just like the chances of a number getting selected exactly once when drawing numbers with replacement. The number of fixed points -- number of people who get their own coat back -- follows a Poisson distribution with mean 1.
The second process seems very different from the first one. It is selection with replacement versus without replacement. But \(e\) is sort of the horizon line of mathematics -- a lot of things tend towards it (or its inverse) in the distance.
Bootstrapping
Say we're working on a typical statistics/machine learning problem. We're given some training data where we already know the right answer, and we're trying to predict for future results. There are a ton of ways we could build a model. Which model will do the best on the unknown data, and how variable might the accuracy be?
Bootstrapping is a way to answer those questions. A good way to estimate how accurate a model will be in the future is to train it over and over with different random subsets of the training data, and see how accurate the model is on the data that was held out. That will give a range of accuracy scores which can be used to estimate how well the model will be on new inputs, where we don't know the answers ahead of time. If the model we're building has a small set of parameters we're fitting (like the coefficients in a linear regression), we can also estimate a range of plausible values for those parameters. If that range is really wide, it indicates a certain parameter isn't that important to the model, because it doesn't matter if it's big or small.
Bootstrapping is a way of answering those questions, using the process described before -- if we have x datapoints, pick x numbers without replacement x times. The ones that get selected at least once are used to train the models, and the ones that don't get selected are used to generate an estimate of accuracy on unseen data. We can do that over and over again and get different splits every time.
It's a fine way to split up the training data and the validation data to generate a range of plausible accuracy scores, but I couldn't find a good reason other than tradition for doing it that way. The 63.2/36.8 split isn't some magical value. Instead of having the numbers that weren't picked be the holdout group, we could instead leave out the numbers that were only picked once (also 1/e of the numbers), and train on the ones not selected or selected more than once. But picking 63% of values (or some other percentage) without replacement is the best way to do it, in my opinion.
The original paper doesn't give any statistical insight into why the choice was made, but a remark at the end says, "it is remarkably easy to implement on the computer", and notes the $4 cost of running the experiments on Stanford's IBM 370/168 mainframe. Maybe it's just the engineer in me, but it seems like a goofy way to do things, unless you actually want a variable number of items selected each run.
In the notebook, I showed that bootstrapping is about 40% slower than selection without replacement when using numpy's choice() function. However, the cost of selecting which items to use for training vs. testing should be insignificant compared to the cost of actually training the models using that train/test split.
A chance encounter
A quick proof of the chances of being selected exactly once.
Doing x selections with replacement, the chance of a number being chosen as the very first selection (and no other times) is \(\frac{1}{x} * \frac{x-1}{x}^{x-1}\)
There are x possible positions for a number to be selected exactly once. Multiply the above by x, which cancels out 1/x. So the chances of a number being selected exactly once at any position is \((\frac{x-1}{x})^{x-1}\).
Let's try to find a number \(q\) so that \(\lim\limits_{x\to\infty} (\frac{x-1}{x})^{x-1} = e^{q}\).
Taking the log of both sides:
\(q = \lim\limits_{x\to\infty} (x-1) * log(\frac{x-1}{x}) = \lim\limits_{x\to\infty} \frac{log(\frac{x-1}{x})}{1/(x-1)}\)
Let \(f(x) = log(\frac{x-1}{x})\) and \(g(x) = \frac{1}{x-1}\)
By L'Hopital's rule, \(\lim\limits_{x\to\infty} \frac{f(x)}{g(x)} = \lim\limits_{x\to\infty}\frac{f'(x)}{g'(x)}\)
The derivative of a log of a function is the derivative of the function divided by the function itself, so:
\(f'(x) = \frac{d}{dx} log(\frac{x-1}{x}) = \frac{d}{dx} log(1 - \frac{1}{x}) = \frac{\frac{d}{dx}(1-\frac{1}{x})}{1-\frac{1}{x}} =\frac{\frac{1}{x^{2}}}{{1-\frac{1}{x}}} = \frac{1}{x^{2}-x} = \frac{1}{x(x-1)}\)
and
\(g'(x) = \frac{-1}{(x-1)^{2}}\)
Canceling out (x-1) from both, \(\frac{f'(x)}{g'(x)} = \frac{1}{x} * \frac{x-1}{-1} = -1 * \frac{x-1}{x}\).
So \(q = \lim\limits_{x\to\infty} -1 * \frac{x-1}{x} = -1\)
At the limit, the probability of being selected exactly once is \(e^{-1} = \frac{1}{e}\)
References/Further Reading
https://mathworld.wolfram.com/Derangement.html
Great explanation of how to calculate derangements using the inclusion-exclusion principle: https://www.themathdoctors.org/derangements-how-often-is-everything-wrong/
The bible of machine learning introduces bootstrapping, but no talk of why that selection process. https://trevorhastie.github.io/ISLR/ISLR%20Seventh%20Printing.pdf
The original bootstrap paper: https://sites.stat.washington.edu/courses/stat527/s14/readings/ann_stat1979.pdf
