
Song: John Hollenbeck & NDR Big Band, "Entitlement"
I've been messing around with prime numbers, because there are several places where they intersect with both random walks and the arcsine distribution. It's going to take a while to finally tie that bow, though.
So it's a quick one this week: a kinda-cool story, and a kinda-cool graph.
Random Primes
The prime numbers are simple to find, but not easy. They're not randomly distributed, but it's hard to come up with easy ways to find them, and they act like random numbers in certain ways. Why is 47 prime and 57 non-prime? You can't really tell just by looking.
To find the primes, we can write down every number from, say, 1 to 1000. Then we cross out 2, and every number divisible by 2 (4, 6, 8, etc.). Repeat that with 3 (6, 9, 12, etc.), and so on. The numbers left behind are prime. This is the famous Sieve of Eratosthenes -- it's a tedious way to find prime numbers, but it's by far the easiest to understand.
The sieve gave mathematician David Hawkins an idea [1]: what about doing that same process, but randomly? For each number, flip a coin, if it comes up heads, cross the number out. That will eliminate half of the numbers on the first pass. Take the lowest number k that remains and eliminate each of the remaining numbers with probability 1/k. Say it's 4. For each remaining number, we flip a 4 sided die and if it comes up 4, we cross it out.
If we go through all the numbers, what's left over won't look like real prime numbers -- there should be as many even fake primes as odd ones, for starters. But the remaining numbers will be as sparse as the actual prime numbers. As the sample size N heads to infinity, the chances of a random number being a real prime, and being a fake prime, are the same -- 1/log(N).
This is a brilliant way to figure out what we know about prime numbers are due to their density, and what are due to other, seemingly more magical (but still non-random) factors.
Several characteristics of real primes apply to the random primes. And tantalizingly, things that can't be proven about real primes can be proven about the fake ones. It's been conjectured that there are infinitely many pairs of twin primes -- primes that are separated by 2 numbers. An example would be 5 and 7, or 11 and 13. It makes sense for a lot of reasons that there should be an infinite number of twin primes. But mathematicians have been trying to prove it for over 150 years, without success.
Random primes can be odd or even, so the analogy to twin primes would be two random primes that are only one apart, say 5 and 6. It's relatively simple to prove that there are an infinite number of random twin primes [2]. That could easily be fool's gold -- treating the primes like they're randomly distributed gives mathematicians a whole toolbox of statistical techniques to use on them, but they're not random, or arbitrary. They're perfectly logical, and yet still inscrutible, hidden in plain sight.
Largest prime factors of composite numbers
I was intrigued by the largest prime factor of composite (non-prime) numbers. Are there any patterns?
As background, every number can be split into a unique set of prime factors. For instance, the number 24 can be factored into 24 = 8 * 3 = 2 * 2 * 2 * 3. Let's say we knock off the biggest prime factor. We get: 2 * 2 * 2 = 8. The raw numbers rapidly get too big, so I looked at the log of the ratio:
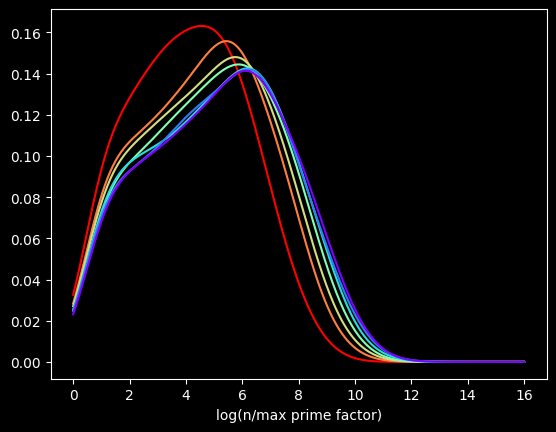
The red curve is the distribution of the first 100,000 composite numbers, the orange is the next 100,000 composite numbers, and so on.
What if we bump up an order of magnitude? This time, the red curve is the first million composite numbers, the orange is the next million, and so on. Here's what that looks like:
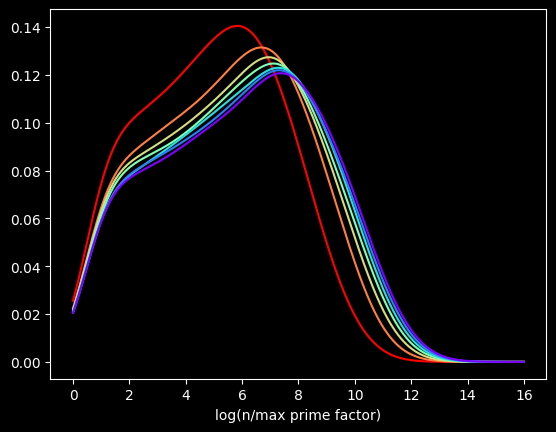
Pretty much the same graph, right? The X axis is different, but the shapes are very similar to the first one.
Let's go another order of magnitude up. The first 10,000,000 versus the next 10,000,000, and so on?
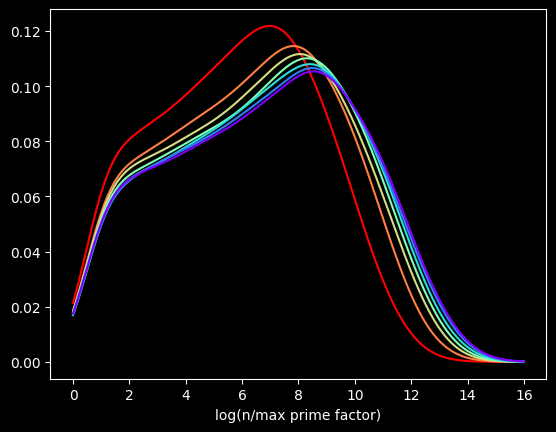
We get the same basic shapes again! The self-similarity is kinda cool. Is it possible to come up with some function for the distribution for this quantity? You tell me.
The perils of interpolation
These graphs are flawed. I'm generating these graphs using Kernel Density Estimation, a technique for visualizing the density of data. Histograms, another common way, can be misleading. The choice of bin size can radically alter what the histogram looks like.
But KDE can also be misleading. These graphs make it look like the curve starts at zero. That's not true. The minimum possible value happens when a number is of the form 2*p, where p is a prime -- the value will be log(2), about .693.
This data is actually way chunkier than KDE is treating it. Every point of data is the log of a whole number. So there aren't that many unique values. For instance, between 0 and 1 on the X axis, there's only one possible value -- log(2). Between 1 and 3, there are only 18 possible values, log(2) thru log(19) -- those being the only integers with a log less than 3 and greater than 1.
This makes it hard to visualize the data accurately. There are too many possible values to display each one individually, but not enough for KDE's smoothing to be appropriate.
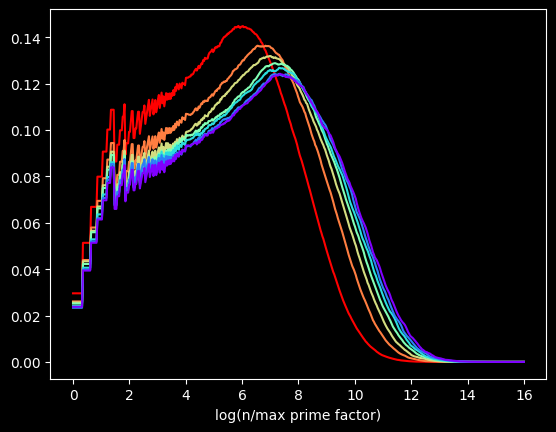
The kernel in Kernel Density Estimation is the algorithm used to smooth the data -- it's basically a moving average that assumes something about the distribution of the data. People usually use the Gaussian kernel, which treats the data like a normal distribution -- smooth and bell curvy. A better choice for chunky data is the tophat kernel, which treats the space between points like a uniform distribution -- in other words, a flat line. If the sparseness of the data on the X axis were due to a small sample size, the tophat kernel would display plateaus that aren't in the real data. But here, I calculated data for the first 100 Million numbers, so there's no lack of data. The sparseness of the data is by construction. log(2) will be the only value between 0 and 1, no matter how many numbers we go up to. So the left side of the graph should look fairly chunky.
The tophat kernel does a much better job of conveying the non-smoothness of the distribution:
References
[1] https://chance.dartmouth.edu/chance_news/recent_news/chance_primes_chapter2.html
[2] for sufficiently large values of simple
[3] https://scikit-learn.org/stable/auto_examples/neighbors/plot_kde_1d.html
[4] https://en.wikipedia.org/wiki/Kernel_density_estimation

Song: Donna Summer and Giorgio Moroder, "I Feel Love" (Patrick Cowley Remix)
Notebook: https://github.com/csdurfee/csdurfee.github.io/blob/main/harmonics.ipynb
I was gonna do random walks this week, but the thing about random walks is you don't know where you're gonna end up, and I ended up back at last week's topic again.
Last time, we saw that the sine wave, sawtooth wave and square wave produced very different distributions.
All three waveforms are used in electronic music, and they all have different acoustic properties. A sine wave sounds like a "boop" -- think of the sound they play to censor someone who says a swear word on the TV. That's a sine wave with a frequency of 1000Hz. Sawtooth waves are extremely buzzy. A square wave has, ironically, kind of a round sound, at least as far as how it gets used in electronic music. A good example is the bass line to this week's song.
It's not a pure square wave, and it's rare to ever hear pure sawtooth or square waves because they're harsh on the ears. Usually multiple waveforms are combined together and then passed through various filters and effects -- in other words, synthesized.
Pretty much every sound you've ever heard is a mix of different frequencies. Only sine waves are truly pure, just a single frequency. I tried looking for an actual musical instrument that produces pure sine waves, and the closest thing (according to the internet, at least) is a tuning fork.
Any other musical instrument, or human voice, or backfiring car, will produce overtones. There's one note that is perceived as the fundamental frequency, but every sound is kind of like a little chord when the overtones are included.
For musical instruments, the loudest overtones are generally at frequencies that are a multiple of the original frequency. These overtones are called harmonics.
For instance, if I play a note at 400 Hz on a guitar, it will also produce harmonics at 800 Hz (2x the fundamental frequency), 1200 Hz (3x), 1600 Hz (4x), 2000 Hz (5x), and so on. This corresponds to the harmonic series in mathematics. It's the sum of the ratios of the wavelengths of the harmonics to the fundamental frequency: 1 + 1/2 + 1/3 + 1/4 + 1/5 + ...
The clarinet is the squarest instrument
I played the clarinet in grade school and I am the biggest dork on the planet, so it's certainly metaphorically true. But it's also literally true.
There's a lot that goes into exactly which overtones get produced by a physical instrument, but most instruments put out the whole series of harmonics. The clarinet is different. Because of a clarinet's physical shape, it pretty much only produces odd harmonics. So, in our example, 400 Hz, 1200 Hz, 2000 Hz, etc.
The square wave is like an idealized version of a clarinet -- it also only puts out odd harmonics. This is a result of how a square wave is constructed. In the real world, they're formed out of a combination of sine waves. Which sine waves? You guessed it -- the ones that correspond to the odd harmonic frequencies.
Here's the fundamental frequency combined with the 3rd harmonic:
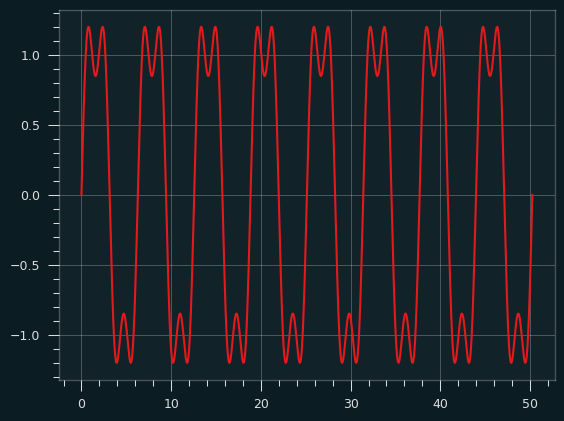
It already looks a bit square-wavey. Additional harmonics make the square parts a bit more square. Here's what it looks like going up to the 19th harmonic:
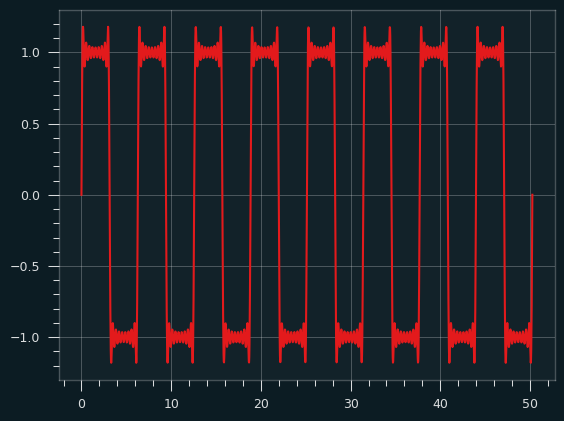
In the real world, we can only add a finite number of harmonics, but if we could combine an infinite number of them, we would get the ideal square wave. This is called the Fourier series of the square wave.
Here's an illustration to help show how the square wave gets built up:
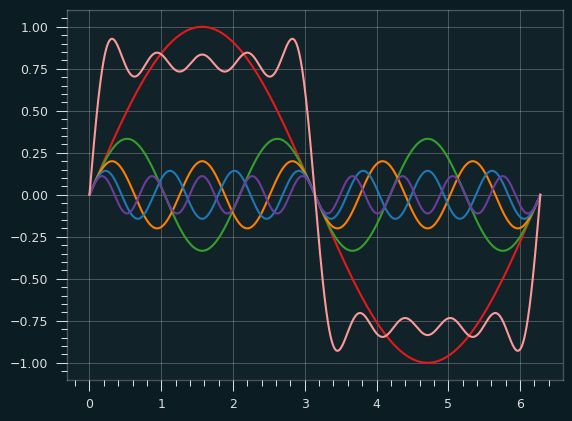
The red wave is the fundamental frequency. The orange square-ish wave is the result of combining the other colored waves with the red wave.
The sum normally would be scaled up a bit (multiplied by 4/pi), but it's easier without the scaling to see how the other waves sort of hammer the fundamental frequency into the shape of the square wave. At some points they are pushing it up, and other points pulling it down.
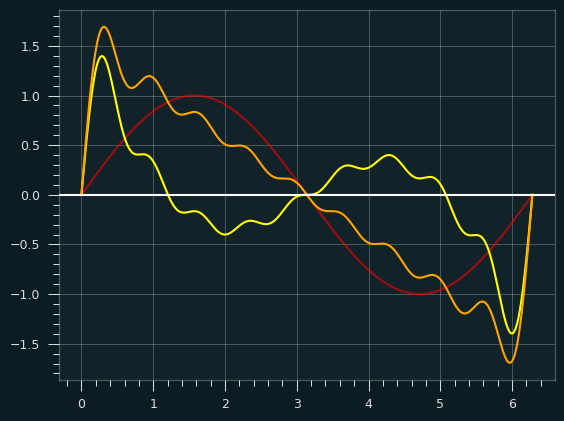
Perhaps this graph makes it clearer. The red is the fundamental, the yellow is the sum of all the other harmonics, and the orange is the combination of the two:
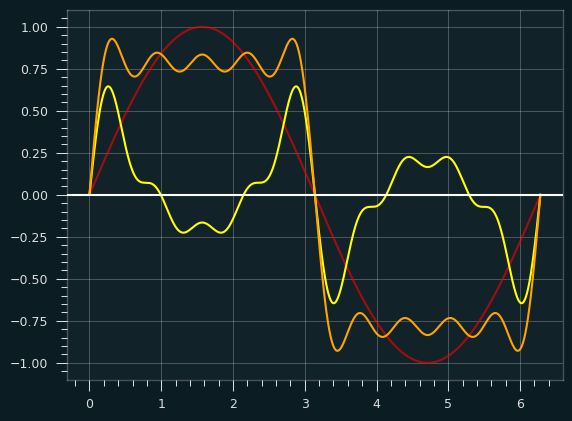
Where the yellow is above the X axis, it's pulling the fundamental frequency up, and where it's below, it's pulling the fundamental down.
The sawtooth
A sawtooth wave is what you get when you combine all the harmonics, odd and even. Like the square wave, it starts to take its basic shape right away. Here's the fundamental plus the second harmonic:
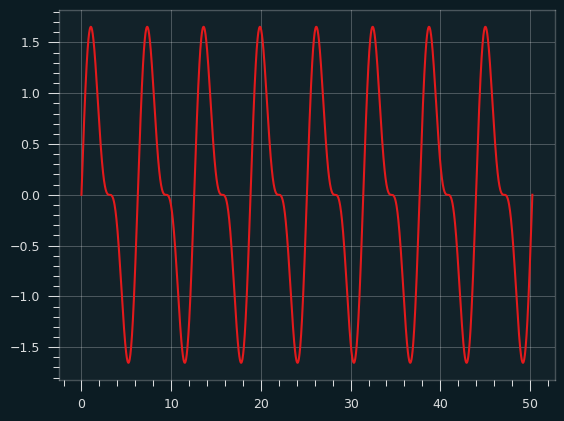
And here it is going all the way up to the 10th harmonic:
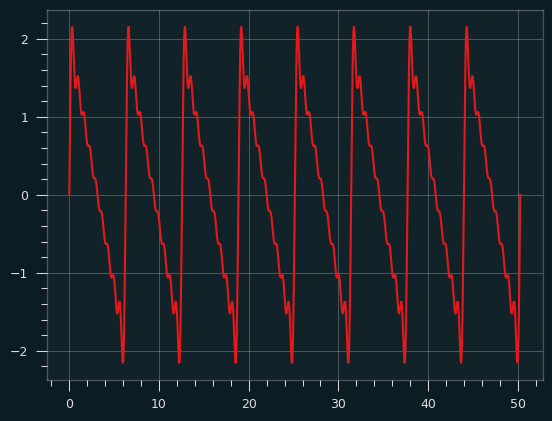
Red fundamental plus yellow harmonics produce the orange sawtooth wave:
Last time, I talked about the sawtooth wave producing a uniform distribution of amplitudes -- the butter gets spread evenly over the toast. The graph above isn't a very smooth stroke of butter. It's not steadily decreasing, particularly at the ends. Here's what the distribution looks like at this point:
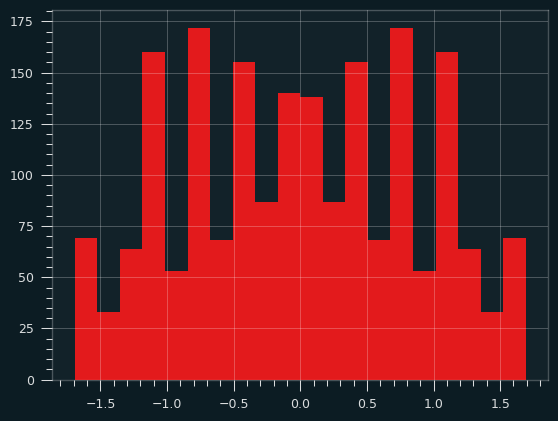
With an infinite series of harmonics, that graph will even out to a uniform distribution
Getting even
What about only the even harmonics? Is that a thing? Not in the natural world as far as I know, but there's nothing stopping me from making one. (It wouldn't be the worst musical crime I've ever committed.)
Here's what a combo of just the even harmonics looks like:
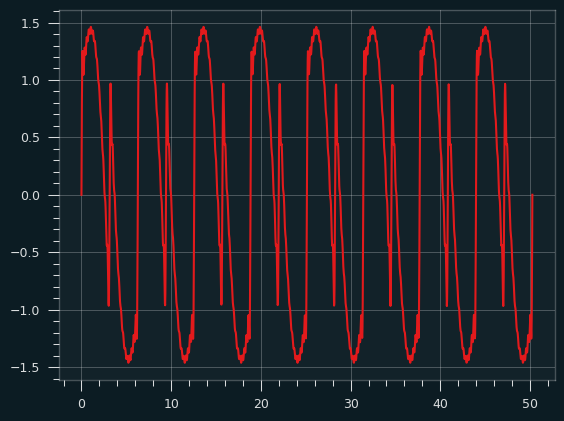
Thanks to a little code from the pygame project, it's easy to turn that waveform into a sound file. It sounds like an angry computer beep, with a little flutter mixed in.
Here's an audio sample
In my prime
The harmonic series of primes is what it sounds like: the harmonic series, but just the prime numbers: 1 + 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + 1/13 + ....
Although it's important in mathematics, I don't have a good musical reason to do this. But if you can throw the prime numbers into something, you gotta do it.
As a sound, I kinda like it. It's nice and throaty. Here's what it sounds like.
It doesn't really sound like a sawtooth wave or a square wave to me. Here's the waveform:
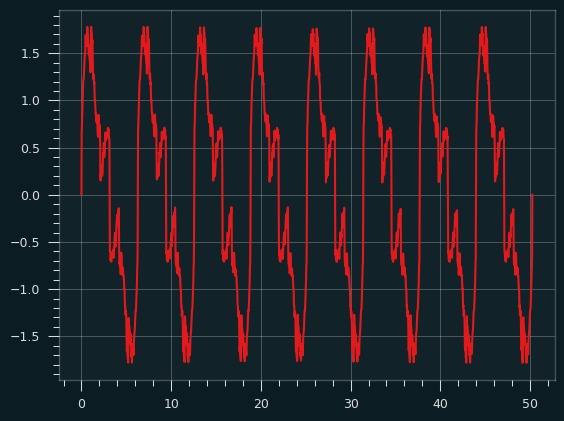
Here's what the distribution of amplitudes looks like:
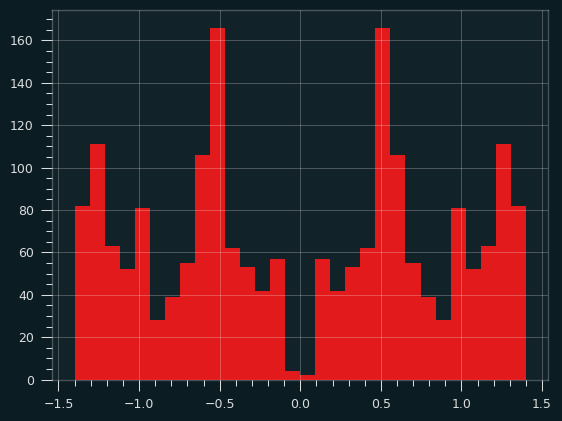
Dissonance
Some of the overtones of the harmonic series don't correspond with the 12 notes of the modern western musical scale (called 12 tone equal temprament, or 12TET). The first 4 harmonics of the series are nice and clean, but after that they get weird. Each harmonic in the series is smaller in amplitude than the previous one, so it has less of an effect on the shape of the final wave. So the dissonance is there, but it's way in the background.
The prime number bloop I made above should be extra weird. The 2nd and 3rd harmonics are included, so those will sound nice, but after that they are at least a little off the standard western scale.
Say we're playing the prime bloop at A4 (the standard pitch used for tuning). Here's how the harmonics work out. A cent is 1% of a semitone. So a note that is off by 50 cents is right between two notes on the 12 tone scale.
| harmonic # |
frequency |
pitch |
error |
| 1 |
440 Hz |
A4 |
0 |
| 2 |
880 Hz |
A5 |
0 |
| 3 |
1320 |
E6 |
+2 cents |
| 5 |
2200 |
C#7 |
-14 cents |
| 7 |
3080 |
G7 |
+31 cents |
| 11 |
4840 |
D#8 |
-49 cents |
| 13 |
5720 |
F8 |
+41 cents |
| 17 |
7480 |
A#8 |
+5 cents |
(Note the 3rd harmonic, E6, is a little off in 12TET, despite being a perfect fifth -- an exact 3:2 ratio with the A5.)
Harmonics aren't everything
While it's true that any audio can be decomposed into a bunch of sine waves, the fundamental frequency and the harmonics aren't really what gives an instrument its unique timbre. It's hundreds or thousands of tiny overtones that don't line up with the harmonics.
Here are the spectra of two different piano sounds playing at 220 Hz. One is a somewhat fake piano sound (Fruity DX10), the other a natural, rich sounding one (LABS Soft Piano, which you might've heard before if you listen to those "Lofi Hip Hop Beats to Doomscroll/Not Study To" playlists). Can you guess which is which?
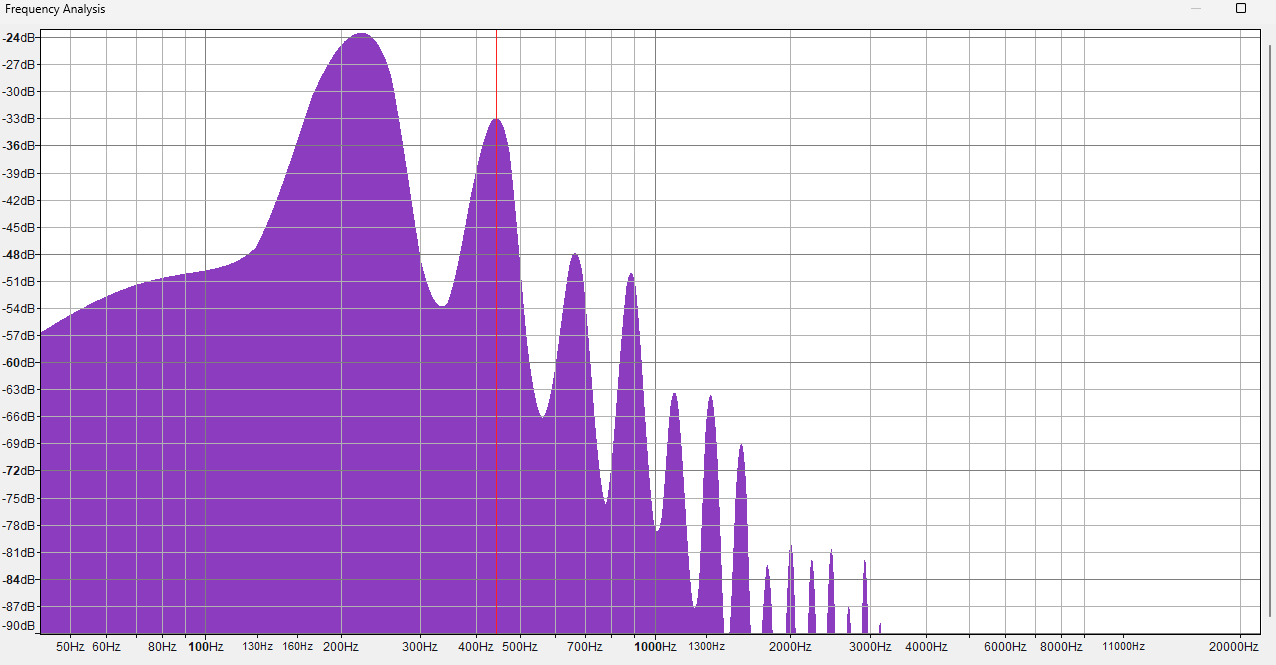
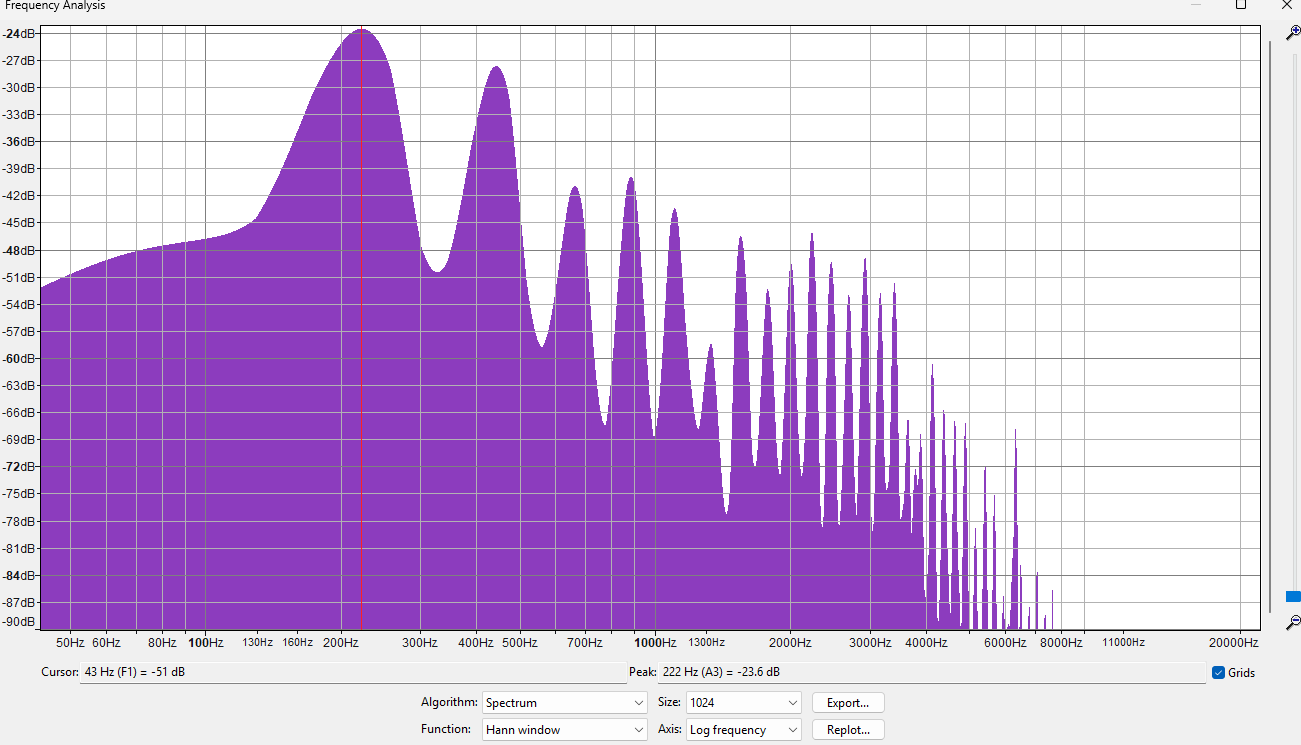
The answer may surprise you. I mean, it can't be that surprising since there are only 2 options. But I'd probably get it wrong, if I didn't already know which is which.
Sources/Notes
This website from UNSW was invaluable, particularly https://newt.phys.unsw.edu.au/jw/harmonics.html
Code used to generate the audio: https://stackoverflow.com/questions/56592522/python-simple-audio-tone-generator
"The internet" claiming the sound of a tuning fork is a sine wave here (no citation given): https://en.wikipedia.org/wiki/Tuning_fork#Description.
There are many good videos on Youtube about 12TET and Just Intonation, by people who know more about music than me. Here's one from David Bennett: https://www.youtube.com/watch?v=7JhVcGtT8z4


















