Sep 10, 2025

Song: Klonhertz, "Three Girl Rhumba"
Notebook available here
Think of a number
Pick a number between 1-100.
Say I write down the numbers from 1-100 on pieces of paper and put them in a big bag, and randomly select from them. After every selection, I put the paper back in the bag, so the same number can get picked more than once. If I do that 100 times, what is the chance of your number being chosen?
The math isn't too tricky. It's often easier to calculate the chances of a thing not happening, then subtract that from 1, to get the chances of the thing happening. There's a 99/100 chance your number doesn't get picked each time. So the probability of never getting selected is \((99/100)^{100} = .366\). Subtract that from one, and there's a 63.4% chance your number will be chosen. Alternately, we'd expect to get 634 unique numbers in 1000 selections.
When I start picking numbers, there's a low chance of getting a duplicate, but that increases as I go along. On my second pick, there's only a 1/100 chance of getting a duplicate. But if I'm near the end and have gotten 60 uniques so far, there's a 60/100 chance.
It's kind of a self-correcting process. Every time I pick a unique number, it increases the odds of getting a duplicate on the next pick. Each pick is independent, but the likelihood of getting a duplicate is not.
I could choose the numbers by flipping a biased coin that comes up heads 63.4% of the time for each one instead. I will get the same number of values on average, and they will be randomly chosen, but the count of values will be much more variable:
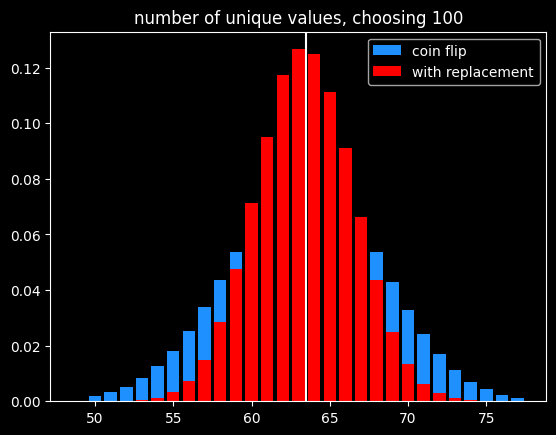
Of course, if the goal is to select exactly 63 items out of 100, the best way would be to randomly select 63 without replacement so there is no variation in the number of items selected.
A number's a number
Instead of selecting 100 times from 100 numbers, what if we selected a bajillion times from a bajillion numbers? To put it in math terms, what is \(\lim\limits_{n\to\infty} (\frac{n-1}{n})^{n}\) ?
It turns out this is equal to \(\frac{1}{e}\) ! Yeah, e! Your old buddy from calculus class. You know, the \(e^{i\pi}\) guy?
As n goes to infinity, the probability of a number being selected is \(1-\frac{1}{e} = .632\). This leads to a technique called bootstrapping, or ".632 selection" in machine learning (back to that in a minute).
Don't think of an answer
What are the chances that a number gets selected exactly once? Turns out, it's \(\frac{1}{e}\), same as the chances of not getting selected! This was surprising enough to me to bother to work out the proof, given at the end.
That means the chances of a number getting selected more than once is \(1 - \frac{2}{e}\).
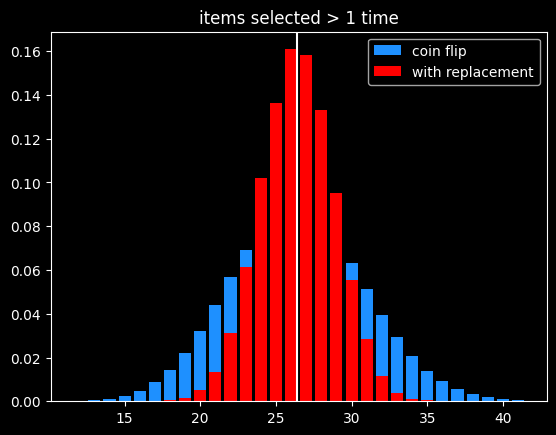
The breakdown:
- 1/e (36.8%) of numbers don't get selected
- 1/e (36.8%) get selected exactly once
- 1-2/e (26.4%) get selected 2+ times
As before, the variance in number of items picked 2+ times is much lower than flipping a coin that comes up heads 26.4% of the time:
Derangements
Say I'm handing out coats randomly after a party. What are the chances that nobody gets their own coat back?
This is called a derangement, and the probability is also 1/e. An almost correct way to think about this is the chance of each person not getting their own coat (or each coat not getting their own person, depending on your perspective) is \(\frac{(x-1)}{x}\) and there are \(x\) coats, so the chances of a derangement are \(\frac{x-1}{x}^{x}\).
This is wrong because each round isn't independent. In the first case, we were doing selection with replacement, so a number being picked one round doesn't affect its probability of being picked next round. That's not the case here. Say we've got the numbers 1 thru 4. To make a derangement, the first selection can be 2, 3 or 4. The second selection can be 1, 3 or 4. But 3 or 4 might have been picked in the first selection and can't be chosen again. 2/3rds of the time, there will only be two options for the second selection, not three.
The long way 'round the mountain involves introducing a new mathematical function called the subfactorial, denoted as \(!x\), which is equal to the integer closest to \(\frac{x!}{e}\). \(e\) gets in there because in the course of counting the number of possible derangements, a series is produced that converges to \(1/e\).
The number of derangements for a set of size x is \(!x\) and the number of permutations is \(x!\), so the probability of a derangement as x gets big is \(\frac{!x}{x!} = \frac{1}{e}\)
What about the chances of only one person getting their coat back? It's also \(\frac{1}{e}\), just like the chances of a number getting selected exactly once when drawing numbers with replacement. The number of fixed points -- number of people who get their own coat back -- follows a Poisson distribution with mean 1.
The second process seems very different from the first one. It is selection with replacement versus without replacement. But \(e\) is sort of the horizon line of mathematics -- a lot of things tend towards it (or its inverse) in the distance.
Bootstrapping
Say we're working on a typical statistics/machine learning problem. We're given some training data where we already know the right answer, and we're trying to predict for future results. There are a ton of ways we could build a model. Which model will do the best on the unknown data, and how variable might the accuracy be?
Bootstrapping is a way to answer those questions. A good way to estimate how accurate a model will be in the future is to train it over and over with different random subsets of the training data, and see how accurate the model is on the data that was held out. That will give a range of accuracy scores which can be used to estimate how well the model will be on new inputs, where we don't know the answers ahead of time. If the model we're building has a small set of parameters we're fitting (like the coefficients in a linear regression), we can also estimate a range of plausible values for those parameters. If that range is really wide, it indicates a certain parameter isn't that important to the model, because it doesn't matter if it's big or small.
Bootstrapping is a way of answering those questions, using the process described before -- if we have x datapoints, pick x numbers without replacement x times. The ones that get selected at least once are used to train the models, and the ones that don't get selected are used to generate an estimate of accuracy on unseen data. We can do that over and over again and get different splits every time.
It's a fine way to split up the training data and the validation data to generate a range of plausible accuracy scores, but I couldn't find a good reason other than tradition for doing it that way. The 63.2/36.8 split isn't some magical value. Instead of having the numbers that weren't picked be the holdout group, we could instead leave out the numbers that were only picked once (also 1/e of the numbers), and train on the ones not selected or selected more than once. But picking 63% of values (or some other percentage) without replacement is the best way to do it, in my opinion.
The original paper doesn't give any statistical insight into why the choice was made, but a remark at the end says, "it is remarkably easy to implement on the computer", and notes the $4 cost of running the experiments on Stanford's IBM 370/168 mainframe. Maybe it's just the engineer in me, but it seems like a goofy way to do things, unless you actually want a variable number of items selected each run.
In the notebook, I showed that bootstrapping is about 40% slower than selection without replacement when using numpy's choice() function. However, the cost of selecting which items to use for training vs. testing should be insignificant compared to the cost of actually training the models using that train/test split.
A chance encounter
A quick proof of the chances of being selected exactly once.
Doing x selections with replacement, the chance of a number being chosen as the very first selection (and no other times) is
\(\frac{1}{x} * \frac{x-1}{x}^{x-1}\)
There are x possible positions for a number to be selected exactly once. Multiply the above by x, which cancels out 1/x. So the chances of a number being selected exactly once at any position is \((\frac{x-1}{x})^{x-1}\).
Let's try to find a number \(q\) so that \(\lim\limits_{x\to\infty} (\frac{x-1}{x})^{x-1} = e^{q}\).
Taking the log of both sides:
\(q = \lim\limits_{x\to\infty} (x-1) * log(\frac{x-1}{x}) = \lim\limits_{x\to\infty} \frac{log(\frac{x-1}{x})}{1/(x-1)}\)
Let
\(f(x) = log(\frac{x-1}{x})\)
and
\(g(x) = \frac{1}{x-1}\)
By L'Hopital's rule, \(\lim\limits_{x\to\infty} \frac{f(x)}{g(x)} = \lim\limits_{x\to\infty}\frac{f'(x)}{g'(x)}\)
The derivative of a log of a function is the derivative of the function divided by the function itself, so:
\(f'(x) = \frac{d}{dx} log(\frac{x-1}{x}) = \frac{d}{dx} log(1 - \frac{1}{x}) = \frac{\frac{d}{dx}(1-\frac{1}{x})}{1-\frac{1}{x}} =\frac{\frac{1}{x^{2}}}{{1-\frac{1}{x}}} = \frac{1}{x^{2}-x} = \frac{1}{x(x-1)}\)
and
\(g'(x) = \frac{-1}{(x-1)^{2}}\)
Canceling out (x-1) from both, \(\frac{f'(x)}{g'(x)} = \frac{1}{x} * \frac{x-1}{-1} = -1 * \frac{x-1}{x}\).
So \(q = \lim\limits_{x\to\infty} -1 * \frac{x-1}{x} = -1\)
At the limit, the probability of being selected exactly once is \(e^{-1} = \frac{1}{e}\)
References/Further Reading
https://oeis.org/A068985
https://mathworld.wolfram.com/Derangement.html
Great explanation of how to calculate derangements using the inclusion-exclusion principle: https://www.themathdoctors.org/derangements-how-often-is-everything-wrong/
The bible of machine learning introduces bootstrapping, but no talk of why that selection process. https://trevorhastie.github.io/ISLR/ISLR%20Seventh%20Printing.pdf
The original bootstrap paper: https://sites.stat.washington.edu/courses/stat527/s14/readings/ann_stat1979.pdf
Aug 08, 2025

Song: The Impressions, "Do You Wanna Win?"
(This is an excerpt from a larger project about sports gambling. Code used, and early drafts of some of the chapters can be found at https://github.com/csdurfee/book.)
I'm going to return to the subject of sports betting this week. Let's start with something easy. How do you avoid going broke betting on sports? That's easy. Reduce your bet size to zero. Scared money don't lose none.
As long as there is randomness, there will be outliers and unexpected results. It is impossible to escape randomness in sports betting. Any time you decide to bet, you enter the kingdom of randomness and have to abide by its laws. It doesn't matter whether you have an advantage over the house (unless the advantage is truly massive). Nothing is guaranteed.
This is a pretty hard thing for us to know how to deal with, when our brains are pattern-finding machines. Our brains will find patterns to give us a sense of control.
Notes
I talk about "win rate" a bunch below. That means the percent of the time a gambler can win bets at even odds (such as a standard spread bet on the NBA or NFL.)
The random walks shown below are a little different from a standard one, because I'm simulating the vig. The walker goes 1 block north when the coin comes up heads (or they win the bet), and 1.1 blocks south when the coin comes up tails (or they lose the bet.)
In the marches of madness
The NCAA holds the March Madness tournament every year to determine who the best college basketball team is. It's a single elimination tournament of 64 teams, arranged into a big bracket.
Say we do a March Madness style bracket with coin flippers instead of basketball teams. We randomly assign them places in the bracket. For each matchup, the coin flipper at the top of the matchup flips a coin. If they get heads, they survive and advance. If they get tails, they lose.
Somebody's going to go 6-0 and win that tournament.
Now imagine we expanded that to every single person on the planet. Every single person gets matched up into a 64 person bracket, then each of those winners get added to another 64 team bracket, and so on.
Eventually, someone has to emerge the victor with a 32-0 record or something -- the greatest coin flipper in the world. Right?
Random walks
Imagine going on a walk. Every time you get to an intersection, you flip a coin. If it's heads, you go one block north and one block east. If it's tails, you go one block south and one block east. This is called a random walk. It's a bit like a gambler's profits or losses plotted on a graph as a function of time.
I think there's a huge value in knowing what random walks look like. Do they remind you of anything?
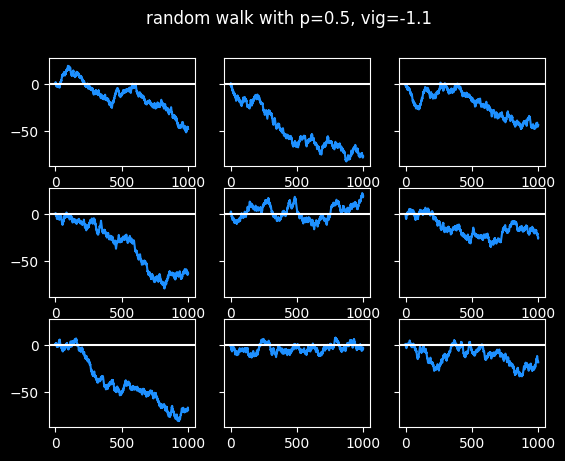
Touts are people who sell recommendations about which bets to take. Pay $30 and they'll tell you which side to bet on the big game tonight. (I have a whole section about touts in the book.) The best tout I could find has had pretty steady success for nearly 20 years, with a win rate of 54.1% against the standard vig. That's statistically significant, but it's not enough to guarantee success moving forwards. Even if they continue to place bets that should win 54.1% of the time -- they're flipping a slightly biased coin -- that doesn't mean they'll make money on those bets. Let's look at some random walks at 54.1% win rate:
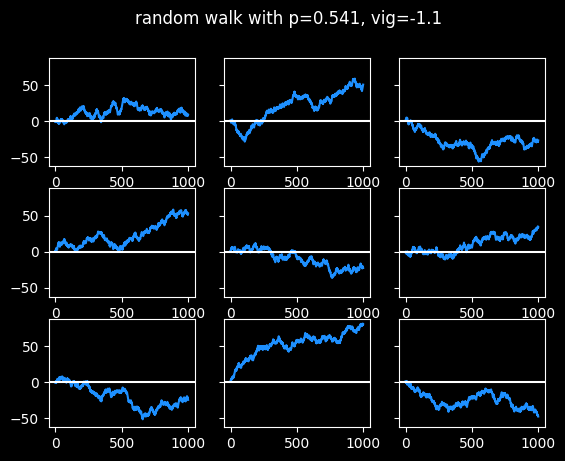
Three of the random walks ended up around 50 units after 1000 bets, which is pretty good. Two of them made a tiny bit of money. The other four lost money. This is a small sample size, but a 44% chance of losing money after paying for 1,000 picks at $30 a pop isn't great. (More info on the economics of touts in the book.)
The touts I looked at generally don't sell picks for every single game. So with 1200 games in an NBA season, this could be several years' worth of results.
Imagine all of these as 9 different touts, with the exact same level of skill at picking games. But some of them look like geniuses, and some look like bozos. There would probably be some selection bias. The ones with the bad records would drop out -- who's buying their picks if they're losing money? And the ones who did better than their true skill level of 54.1% would be more likely to stick with it. Yet all these random walks were generated with the same 54.1% win rate.
If you bought 1,000 picks from this tout, you don't get to choose which of the \(2^{1000} = (2^{10})^{100} \approx 10^{300}\) possible random walks you will actually get. If each bet has a 54.1% chance of winning, there's no guarantee you will have exactly 541 wins and 459 losses at the end of 1000 bets.
Here's what someone who is right 60% of the time looks like.
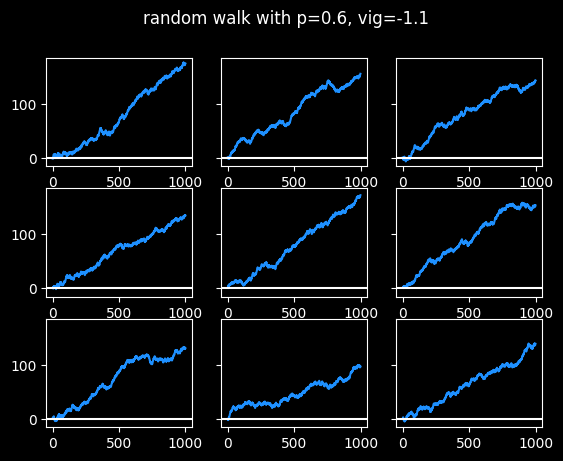
Success is pretty boring.
I've always said it's much harder to learn from success than from failure. At a 60% win rate, none of them really have long cold streaks, just small breaks between hot streaks. It wouldn't be interesting to tell stories about those graphs. There's nothing to learn, really.
I don't think it's possible to win 60% against the spread, based on what are called push charts, discussed in the book.
The graphs at the 54.1% success rate appear a lot more human. They have hot and cold streaks, swoons, periods where they seem stuck in a range of values. Some of them scuffled the whole time, a couple finally got locked in near the end, a couple were consistently good. Some had good years, some had bad years. Even though they are randomly generated, they look like they have more to teach us, like they offer more opportunities to tell stories. But they all have the exact same win rate, or level of skill at handicapping.
No outcome is guaranteed, but the higher the win rate, the more consistently the graph is going to go up and to the right at a steady pace.
Finally, here are some walks at 52.4% win rate, the break-even point. Most results end up close to zero after 1000 bets, but there is always a possibility of an extended run towards the positive or negative side -- it happened 4/9 times in this sample:
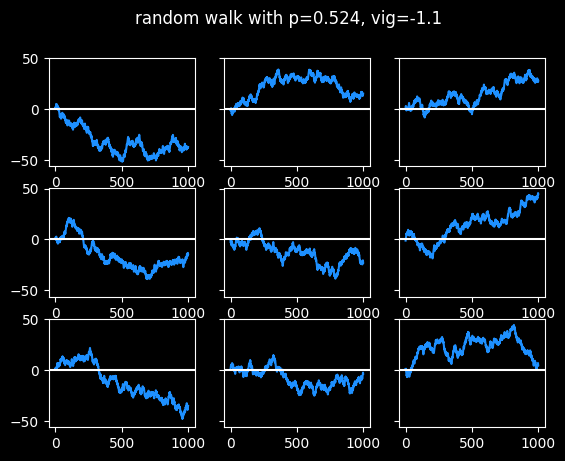
The Axe Forgets, The Tree Remembers
If those 9 graphs were stock prices, which one would you consider the best investment?
Well, we know they're equally bad investments. They're winning just enough to break even, but not make profits.
They all have the same Expected Value moving forwards. Previous results are meaningless and have no bearing on whether the next step will be up or down. Every step is the start of an entirely new random walk. The coin doesn't remember what has happened in the past. We do.
This is what's known in math as a Martingale, named after a betting system that was popular in France hundreds of years ago. (I previously talked about Martingales in the series on the hot hand.)
The basic idea behind all these betting systems is to chase losses by betting more when you're losing. Hopefully it's obvious that these chase systems are crazy, though formally proving it led to a lot of interesting math.
Fallacy and ruin
Even though chase systems are irrational, they've persisted through the centuries. Human beings are wired to be semi-rational -- we use previous data to try and predict the future, but we use it even when the data was randomly generated, and even when we don't have a significant amount of data. We need coherent stories to tell about why things happened. There is no rational reason to believe in a chase system, but I think there are semi-rational reasons to fall prey to the gambler's fallacy.
I hope these random walks show that having a modest, plausible advantage over the house isn't a guarantee of success, even over a really long timespan. Positive Expected Value is necessary, but not sufficient, for making money long term.
The vast majority of gamblers bet with negative expected value due to the vig, and possibly biases in the lines against public teams, as we saw in a previous installment. If each bet the average gambler makes has a negative expected value, they can't fix that by betting MORE.
"If I keep doubling down, eventually I'll win it all back." Maybe if you have infinite capital and unlimited time. Otherwise the Gambler's Ruin is certain. The market can stay liquid longer than you can stay irrational.
Maximizing profits: the Kelly criterion
Let's say a bettor really does have an edge over the house -- they can beat the spreads on NBA basketball 56% of the time.
Even with that advantage, it's easy to go broke betting too much at once. Suppose they bet 25% of their bankroll on each bet. What happens after 200 bets? 200 bets is not a lot, roughly 1 month of NBA games if they bet on every game.
Once in a blue moon they end up a big winner, but 53% of the time the gambler is left with less than 5% of their bankroll after 200 bets even though they have a pretty healthy advantage over the house. So it's still a game of chance rather than skill, even though it would require a lot of mental labor to make the picks, and time to actually bet the picks. The mean rate of return is quite impressive (turning $100 into $4,650), but the median result is bankruptcy (turning $100 into $3).
Intuitively, there has to be some connection between the betting advantage and the optimal amount to risk on each bet. If a gambler only has a tiny advantage, they should only be making tiny bets as a percentage of their total bankroll. The better they are, the more they can risk. And if they have no advantage, they shouldn't bet real money at all.
That intuition is correct. The Kelly criterion gives a formula for the exact percent of the bankroll to risk on each bet in order to maximize Expected Value, given a certain level of advantage. https://en.wikipedia.org/wiki/Kelly_criterion
In this case, the Kelly criterion says to bet 7.6% of the total bankroll on each bet. I did 100,000 simulations of a sequence of 200 bets following the Kelly criterion. The gambler only went broke around one time in 1,000, which is much better. The median result was turning $100 into $168, which is pretty good. However, the gambler still lost money 31% of the time.
This is just one month of betting, assuming the gambler bets on every NBA game. Losing money 31% of the time seems pretty high for what's supposed to be the optimal way to bet.
How about a longer period of time? I simulated 1,000 bets this time, nearly a whole season of the NBA. The median outcome is turning $100 into $1356, which is a sweet rate of return. But the chances of going broke actually increased! The player will go broke 1.4% of the time, about 11x more often on 1000 bets than 200, which seems unfair, but the Kelly criterion doesn't make any guarantees about not going broke. It just offers the way to optimize Expected Value if the gambler knows the exact advantage they have over the house.
Partial Kelly Betting
Kelly Betting is the optimal way to maximize profits, but what about lower stakes? The real power of Kelly betting is its compounding nature -- as the bankroll gets bigger or smaller, the bet size scales up or down as well. It also corresponds to our incorrect intuitive understanding of randomness -- it makes sense someone should bet smaller amounts when they're on a cold streak, and larger amounts when they're on a hot streak.
What if the gambler only bets 2% of their bankroll instead of the 7.6% recommended by the Kelly criterion? They don't go broke a single time in 100,000 simulations of 1,000 bets. The mean rate of return is 4.6x and the median is 3.7x. That's a pretty nice return on investment, relative to the risk. The gambler still lost money 2.8% of the time, though. Being conservative, betting a lot of games at positive expected value, and betting the right way greatly increase the chances of success, but nothing can eliminate the possibility of failure.
Imagine doing 1000 bets at 56% win percentage and a conservative bet size, and still losing money. Wild, isn't it? If you take one thing away from this article, it should be:
Failure is always an option.
Betting a constant amount
You wouldn't have that problem with betting a constant amount, right? Say a gambler has a bankroll of $100 and bets to win $20 on each game. 1000 games, 56 win %.
This Expected Value of playing this way doesn't have any randomness in it. It's just a simple algebra problem. According to EV, they should end up with $252 at the end of the season, for a profit of $152. Nice. But as I've mentioned before, EV says nothing about the range of possible outcomes.
If I actually simulate it, a pretty wide range of outcomes are possible. 99% of the time, the gambler makes money, but 6 times out of 100,000, they lose everything and more. (6 in 100,000 is about the same odds as winning a 14 leg parlay.)
With betting a fixed size, the rate of return is lower and the risk of going broke doesn't go away. So it's sub-optimal compared to Kelly-style betting with a very small percentage of the total bankroll.
Jul 31, 2025

Song: Donna Summer and Giorgio Moroder, "I Feel Love" (Patrick Cowley Remix)
Notebook: https://github.com/csdurfee/csdurfee.github.io/blob/main/harmonics.ipynb
I was gonna do random walks this week, but the thing about random walks is you don't know where you're gonna end up, and I ended up back at last week's topic again.
Last time, we saw that the sine wave, sawtooth wave and square wave produced very different distributions.
All three waveforms are used in electronic music, and they all have different acoustic properties. A sine wave sounds like a "boop" -- think of the sound they play to censor someone who says a swear word on the TV. That's a sine wave with a frequency of 1000Hz. Sawtooth waves are extremely buzzy. A square wave has, ironically, kind of a round sound, at least as far as how it gets used in electronic music. A good example is the bass line to this week's song.
It's not a pure square wave, and it's rare to ever hear pure sawtooth or square waves because they're harsh on the ears. Usually multiple waveforms are combined together and then passed through various filters and effects -- in other words, synthesized.
Pretty much every sound you've ever heard is a mix of different frequencies. Only sine waves are truly pure, just a single frequency. I tried looking for an actual musical instrument that produces pure sine waves, and the closest thing (according to the internet, at least) is a tuning fork.
Any other musical instrument, or human voice, or backfiring car, will produce overtones. There's one note that is perceived as the fundamental frequency, but every sound is kind of like a little chord when the overtones are included.
For musical instruments, the loudest overtones are generally at frequencies that are a multiple of the original frequency. These overtones are called harmonics.
For instance, if I play a note at 400 Hz on a guitar, it will also produce harmonics at 800 Hz (2x the fundamental frequency), 1200 Hz (3x), 1600 Hz (4x), 2000 Hz (5x), and so on. This corresponds to the harmonic series in mathematics. It's the sum of the ratios of the wavelengths of the harmonics to the fundamental frequency: 1 + 1/2 + 1/3 + 1/4 + 1/5 + ...
The clarinet is the squarest instrument
I played the clarinet in grade school and I am the biggest dork on the planet, so it's certainly metaphorically true. But it's also literally true.
There's a lot that goes into exactly which overtones get produced by a physical instrument, but most instruments put out the whole series of harmonics. The clarinet is different. Because of a clarinet's physical shape, it pretty much only produces odd harmonics. So, in our example, 400 Hz, 1200 Hz, 2000 Hz, etc.
The square wave is like an idealized version of a clarinet -- it also only puts out odd harmonics. This is a result of how a square wave is constructed. In the real world, they're formed out of a combination of sine waves. Which sine waves? You guessed it -- the ones that correspond to the odd harmonic frequencies.
Here's the fundamental frequency combined with the 3rd harmonic:
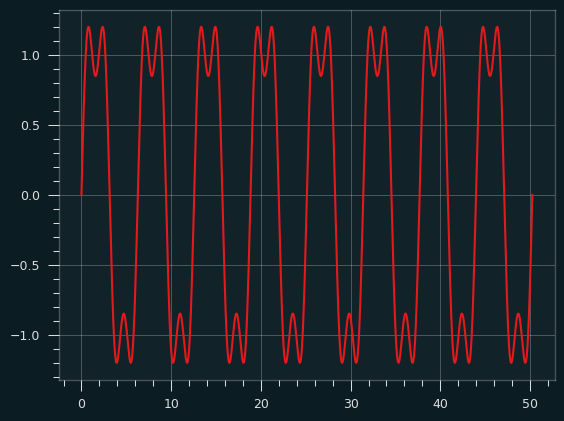
It already looks a bit square-wavey. Additional harmonics make the square parts a bit more square. Here's what it looks like going up to the 19th harmonic:
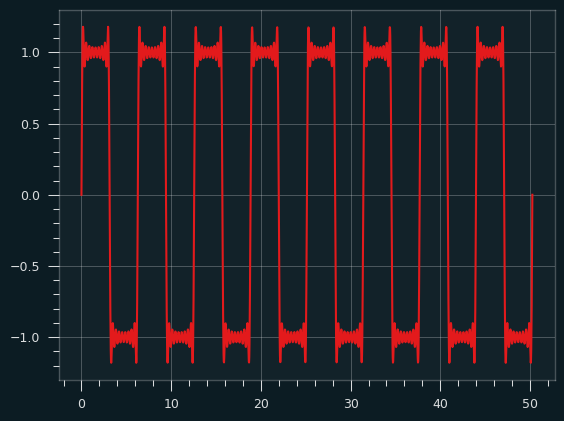
In the real world, we can only add a finite number of harmonics, but if we could combine an infinite number of them, we would get the ideal square wave. This is called the Fourier series of the square wave.
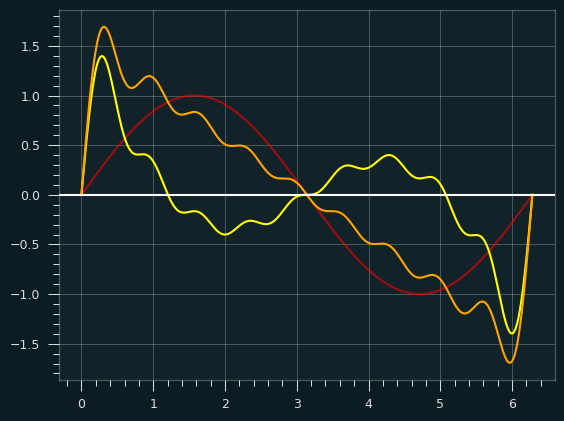
Here's an illustration to help show how the square wave gets built up:
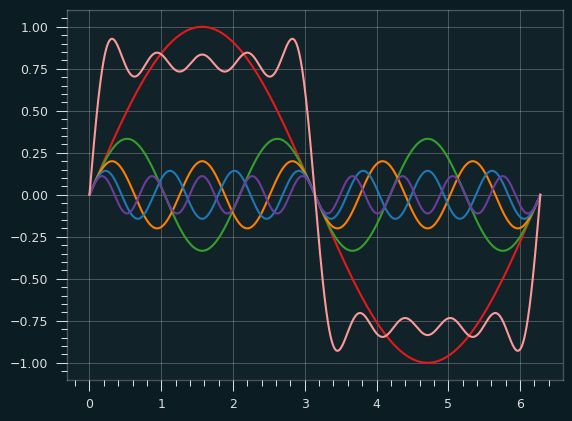
The red wave is the fundamental frequency. The orange square-ish wave is the result of combining the other colored waves with the red wave.
The sum normally would be scaled up a bit (multiplied by 4/pi), but it's easier without the scaling to see how the other waves sort of hammer the fundamental frequency into the shape of the square wave. At some points they are pushing it up, and other points pulling it down.
Perhaps this graph makes it clearer. The red is the fundamental, the yellow is the sum of all the other harmonics, and the orange is the combination of the two:
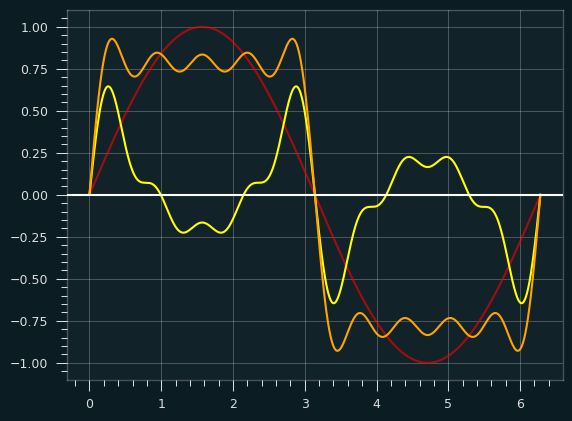
Where the yellow is above the X axis, it's pulling the fundamental frequency up, and where it's below, it's pulling the fundamental down.
The sawtooth
A sawtooth wave is what you get when you combine all the harmonics, odd and even. Like the square wave, it starts to take its basic shape right away. Here's the fundamental plus the second harmonic:
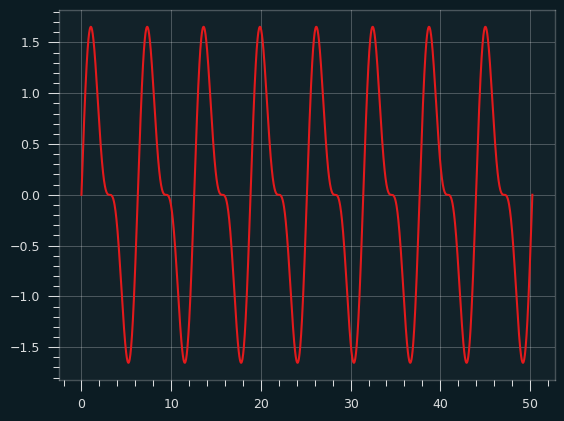
And here it is going all the way up to the 10th harmonic:
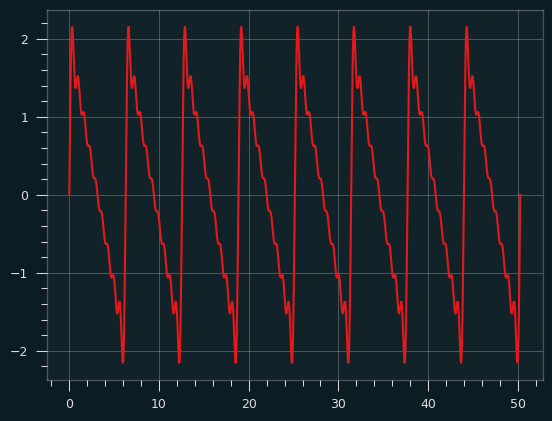
Red fundamental plus yellow harmonics produce the orange sawtooth wave:
Last time, I talked about the sawtooth wave producing a uniform distribution of amplitudes -- the butter gets spread evenly over the toast. The graph above isn't a very smooth stroke of butter. It's not steadily decreasing, particularly at the ends. Here's what the distribution looks like at this point:
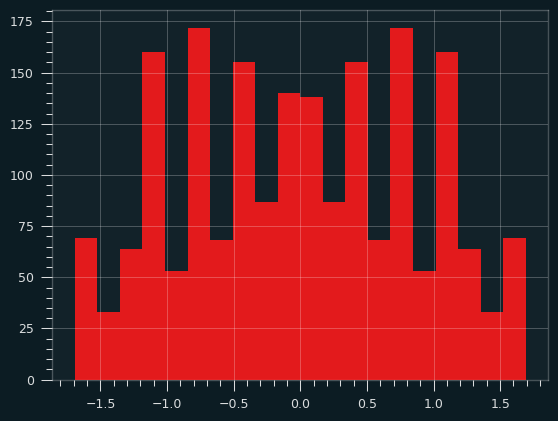
With an infinite series of harmonics, that graph will even out to a uniform distribution
Getting even
What about only the even harmonics? Is that a thing? Not in the natural world as far as I know, but there's nothing stopping me from making one. (It wouldn't be the worst musical crime I've ever committed.)
Here's what a combo of just the even harmonics looks like:
Thanks to a little code from the pygame project, it's easy to turn that waveform into a sound file. It sounds like an angry computer beep, with a little flutter mixed in.
Here's an audio sample
In my prime
The harmonic series of primes is what it sounds like: the harmonic series, but just the prime numbers: 1 + 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + 1/13 + ....
Although it's important in mathematics, I don't have a good musical reason to do this. But if you can throw the prime numbers into something, you gotta do it.
As a sound, I kinda like it. It's nice and throaty. Here's what it sounds like.
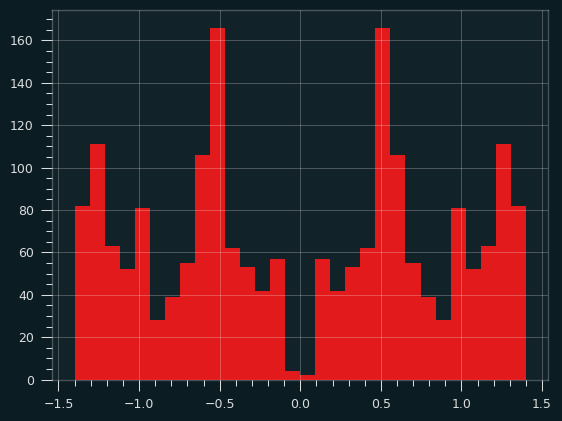
It doesn't really sound like a sawtooth wave or a square wave to me. Here's the waveform:
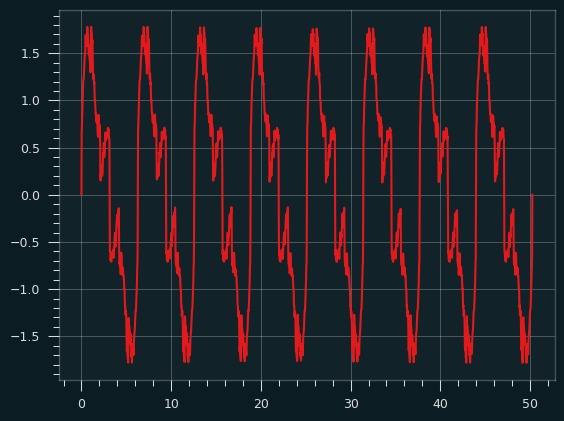
Here's what the distribution of amplitudes looks like:
Dissonance
Some of the overtones of the harmonic series don't correspond with the 12 notes of the modern western musical scale (called 12 tone equal temprament, or 12TET). The first 4 harmonics of the series are nice and clean, but after that they get weird. Each harmonic in the series is smaller in amplitude than the previous one, so it has less of an effect on the shape of the final wave. So the dissonance is there, but it's way in the background.
The prime number bloop I made above should be extra weird. The 2nd and 3rd harmonics are included, so those will sound nice, but after that they are at least a little off the standard western scale.
Say we're playing the prime bloop at A4 (the standard pitch used for tuning). Here's how the harmonics work out. A cent is 1% of a semitone. So a note that is off by 50 cents is right between two notes on the 12 tone scale.
| harmonic # |
frequency |
pitch |
error |
| 1 |
440 Hz |
A4 |
0 |
| 2 |
880 Hz |
A5 |
0 |
| 3 |
1320 |
E6 |
+2 cents |
| 5 |
2200 |
C#7 |
-14 cents |
| 7 |
3080 |
G7 |
+31 cents |
| 11 |
4840 |
D#8 |
-49 cents |
| 13 |
5720 |
F8 |
+41 cents |
| 17 |
7480 |
A#8 |
+5 cents |
(Note the 3rd harmonic, E6, is a little off in 12TET, despite being a perfect fifth -- an exact 3:2 ratio with the A5.)
Harmonics aren't everything
While it's true that any audio can be decomposed into a bunch of sine waves, the fundamental frequency and the harmonics aren't really what gives an instrument its unique timbre. It's hundreds or thousands of tiny overtones that don't line up with the harmonics.
Here are the spectra of two different piano sounds playing at 220 Hz. One is a somewhat fake piano sound (Fruity DX10), the other a natural, rich sounding one (LABS Soft Piano, which you might've heard before if you listen to those "Lofi Hip Hop Beats to Doomscroll/Not Study To" playlists). Can you guess which is which?
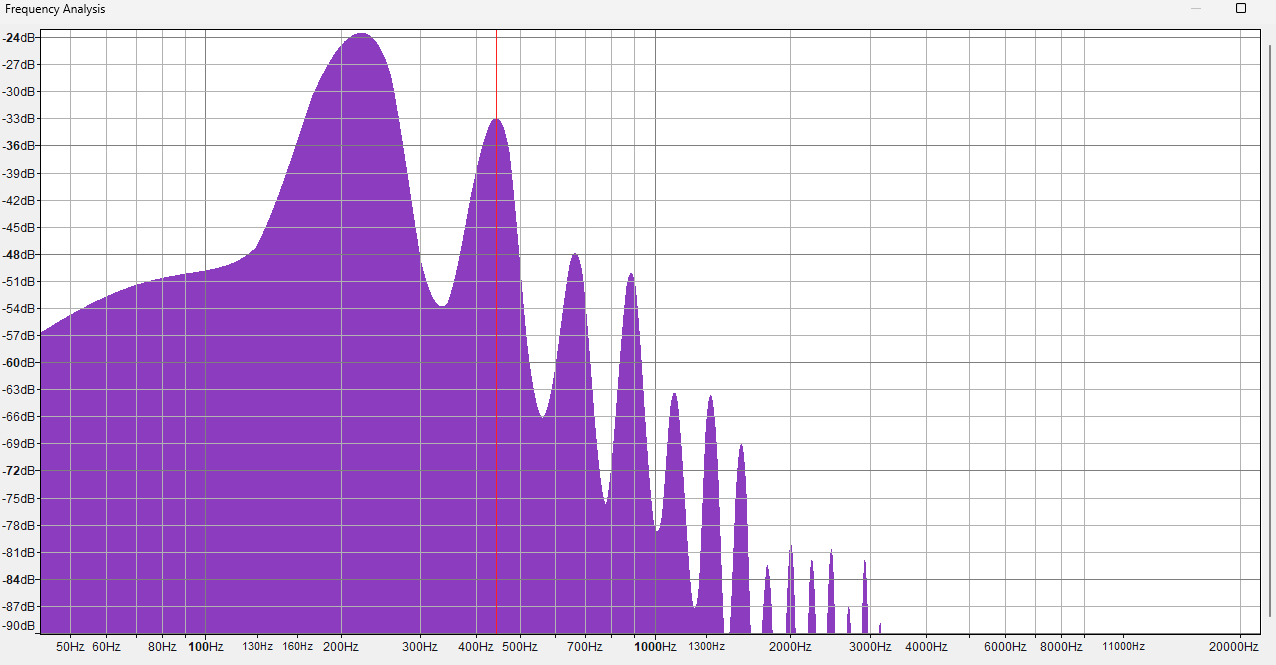
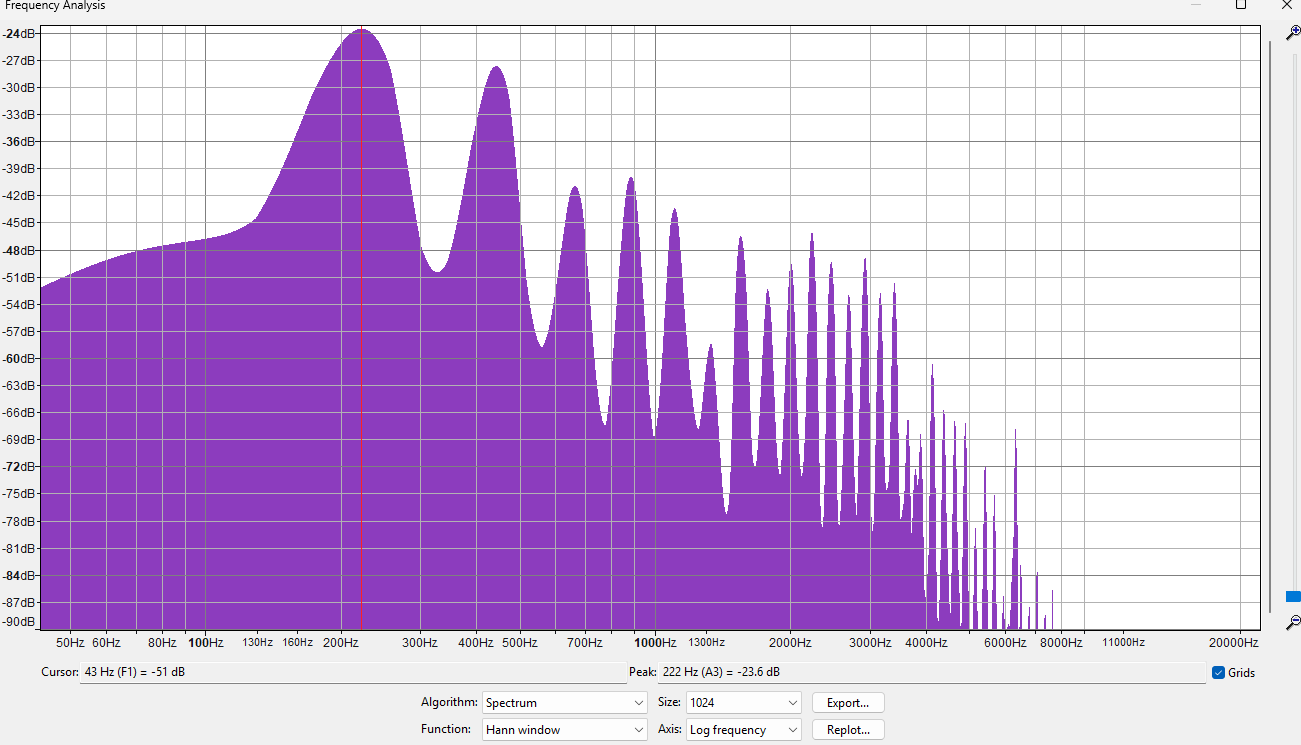
The answer may surprise you. I mean, it can't be that surprising since there are only 2 options. But I'd probably get it wrong, if I didn't already know which is which.
Sources/Notes
This website from UNSW was invaluable, particularly https://newt.phys.unsw.edu.au/jw/harmonics.html
Code used to generate the audio: https://stackoverflow.com/questions/56592522/python-simple-audio-tone-generator
"The internet" claiming the sound of a tuning fork is a sine wave here (no citation given): https://en.wikipedia.org/wiki/Tuning_fork#Description.
There are many good videos on Youtube about 12TET and Just Intonation, by people who know more about music than me. Here's one from David Bennett: https://www.youtube.com/watch?v=7JhVcGtT8z4
Jul 26, 2025

After spending several weeks in the degenerate world of sports gambling, I figured we should go get some fresh air in the land of pure statistics.
The Abnormal Distribution
Everybody knows what the normal distribution looks like, even if they don't know it as such. You know, the bell curve? The one from the memes?
In traditional statistics, the One Big Thing you need to know is called the Central Limit Theorem. It says, if you collect some data and take the average of it, that average (the sample mean) will behave in nice, predictable ways. It's the basis of basically all experimental anything. If you take a bunch of random samples and calculate the sample mean over and over again, those sample means will look like a normal distribution, if the sample sizes are big enough. That makes it possible to draw big conclusions from relatively small amounts of data.
How big is "big enough"? Well, it partly depends on the shape of the data being sampled from. If the data itself is distributed like a normal distribution, it makes sense that the sample means would also be normally shaped. It takes a smaller sample size to get the sampling distributions looking like a normal distribution.
While a lot of things in life are normally distributed, some of them aren't. The uniform distribution is when every possible outcome is equally likely. Rolling a single die, for instance. 1-6 are all equally likely. Imagine we're trying to estimate the mean value for rolling a standard 6 sided die.
A clever way would be to team up sets of sides - 6 goes with 1, 5 goes with 2, 4 goes with 3. Clearly the mean value has to be 3.5, right?
A less clever way would be to roll a 6 sided die a bunch of times and take the average. We could repeat that process, and track all of these averages. If the sample size is big enough, those averages will make a nice bell curve, with the center at 3.5.
The uniform distribution is sort of obnoxious if you want to calculate the sample mean. The normal distribution, and a lot of other distributions, have a big peak in the middle and tail off towards the edges. If you pick randomly from one of these distributions, it's far more likely to be close to the middle than it is to be far from the middle. With the uniform distribution, every outcome is equally likely:
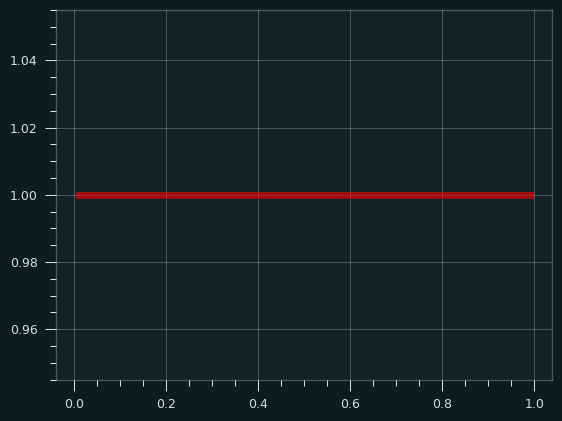
Couldn't we do even worse than the uniform distribution, though? What if the tails/outliers were even higher than the center? When I first learned about the Central Limit Theorem, I remember thinking about that - how could you define a distribution to be the most obnoxious one possible? The normal distribution is like a frowny face. The Uniform distribution is like a "not impressed" face. Couldn't we have a smiley face distribution to be the anti-normal distribution?
Waveforms and probabilities.
All synthesizers in electronic music use a mix of different types of simple waveforms. The sublime TB-303 synth line in the song at the top is very simple. The TB-303 a monophonic synth -- a single sawtooth wave (or square wave) with a bunch of filters on top that, in the right hands, turn it from buzzy electronic noise to an emotionally expressive instrument, almost like a digitial violin or human voice.
This got me thinking about what probability distributions based on different types of waveforms would look like. How likely is the waveform to be at each amplitude?
Here's the sawtooth waveform:
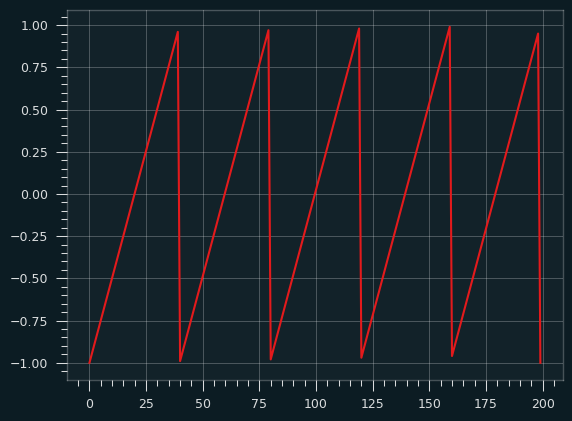
If we randomly sample from this wave (following a uniform distribution -- all numbers on the x axis are equally likely) and record the y value, then plot the values as a histogram, what would it look like? Think of it like we put a piece of toast on the Y axis of the graph, the X axis is time. How will the butter be distributed?
It should be a flat line, like the Uniform distribution, since each stroke of butter is at a constant rate. We're alternating between a very fast wipe and a slower one, but in both cases, it doesn't spend any more time on one section of bread than another because it's a straight line.
Advanced breakfast techniques
A square wave spends almost no time in the middle of the bread, so nearly all the butter will be at the edges. That's not a very interesting graph. What about a sine wave?
The sawtooth wave always has a constant slope, so the butter is evenly applied. With the sine wave, the slope changes over time. Because of that, the butter knife ends up spending more time at the extreme ends of the bread, where the slope is shallow, compared to the middle of the bread. The more vertical the slope, the faster the knife passes over that bit of bread, and the less butter it gets.
If we sample a bunch of values from the sine wave and plot their Y values as a histogram, we'll get something that looks like a smiley face -- lots of butter near the edges, less butter near the center of the toast. Or perhaps, in tribute to Ozzy, the index and pinky fingers of someone throwing the devil horns.
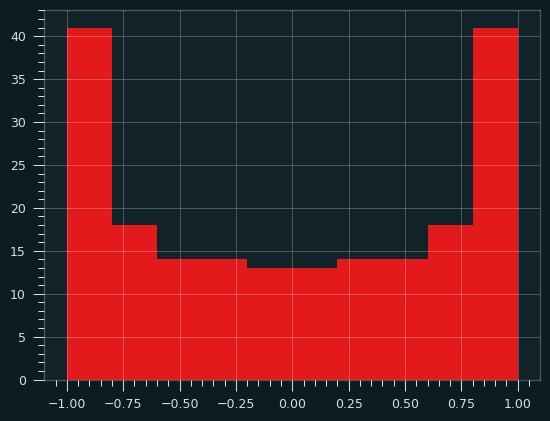
That's a perfectly valid buttering strategy in my book. The crust near the edges tends to be drier, and so can soak up more butter. You actually want to go a bit thinner in the middle, to maintain the structural integrity of the toast.
This distribution of butter forms a probability distribution called the arcsine distribution. It's an anti-normal distribution -- fat in the tails, skinny in the middle. A "why so serious?" distribution the Joker might appreciate. The mean is the least likely value, rather than the most likely value. And yet, the Central Limit Theorem still holds. The mean of even a fairly small number of values will behave like a Normal distribution.
Here are 1,000 iterations of an average of two samples from the arcsine distribution:
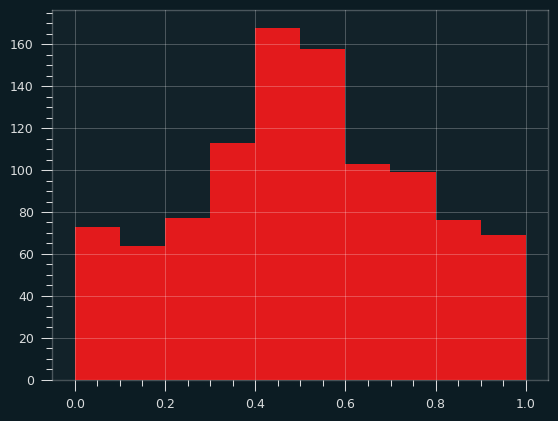
And averages of 5 samples:
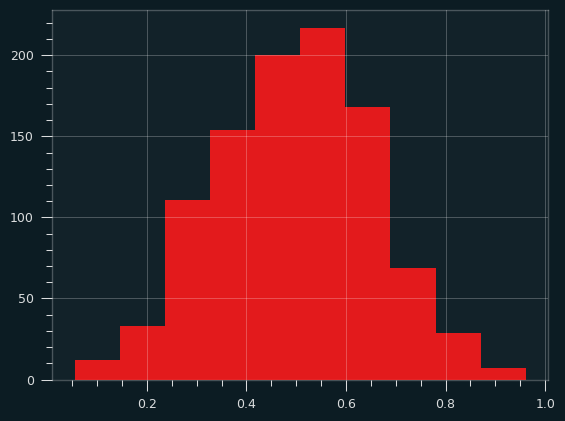
And 30 samples at a time. Notice how the x range has shrunk down.
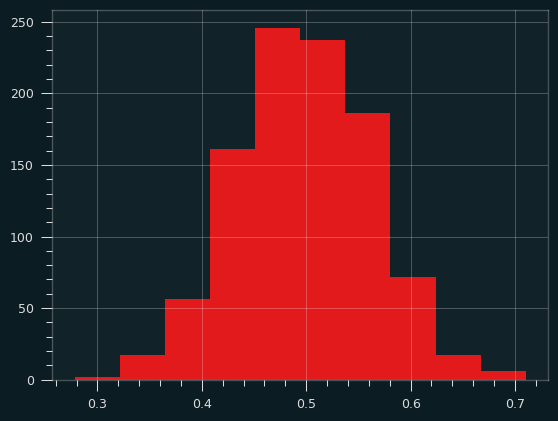
There are a lot of distributions that produce that U-type shape. They're known as bathtub curves. They come up when plotting the failure rates of devices (or people). For a lot of things, there's an elevated risk of failure near the beginning and the end, with lower risk in the middle. The curve is showing conditional probability -- for an iPhone to fail on day 500, it has to have not failed on the first 499 days.

(source: Wikipedia/Public Domain, https://commons.wikimedia.org/w/index.php?curid=7458336)
Particle man vs triangle man
The Uniform distribution isn't really that ab-Normal. It's flat, but it's very malleable. It turns into the normal distribution almost instantly. The symmetry helps.
If we take a single sample from a Uniform distribution over and over again, and plot a histogram, it's going to look flat, because every outcome is equally likely.
If we take the sum (or average) of two Uniform random variables, what would that look like? We're going to randomly select two numbers between 0 and 1 and sum them up. The result will be between 0 and 2. But some outcomes will be more likely than others. The extremes (0 and 2) should be extremely unlikely, right? Both the random numbers would have to be close to 0 for the sum to be, and vice versa. There are a lot of ways to get a sum of 1, though. It could be .9 and .1, or .8 and .2, and so on.
If you look online, you can find many explanations of how to get the PDF of the sum of two Uniform distributions using calculus. (Here's a good one). While formal proofs are important, it's not very intuitive. So, here's another way to think of it.
Let's say we're taking the sum of two dice instead of two Uniform random variables. We're gonna start with two 4 sided dice. It will be obvious that we can scale the number of faces up, and the pattern will hold.
What are the possible combinations of dice? The dice are independent, so each combination is equally likely. Let's write them out by columns according to their totals:
|
|
|
|
|
|
|
| (1, 1) |
(1,2) |
(1,3) |
(1,4) |
- |
- |
- |
| - |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
- |
- |
| - |
- |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
- |
| - |
- |
- |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
If we write all the possibilities out like this, it's gonna look like a trapezoid, whether there are 4 faces on the dice, or 4 bajillion. Each row will have one more column that's blank than the one before, and one column that's on its own off to the right.
If we consolidate the elements, we're gonna get a big triangle, right? Each column up to the mean will have one more combo, and each column after will have one less.
|
|
|
|
|
|
|
| (1, 1) |
(1,2) |
(1,3) |
(1,4) |
(2,4) |
(3,4) |
(4,4) |
| - |
(2,1) |
(2,2) |
(2,3) |
(3,3) |
(4,3) |
- |
| - |
- |
(3,1) |
(3,2) |
(4,2) |
- |
- |
| - |
- |
- |
(4,1) |
- |
- |
- |
With a slight re-arrangement of values, it's clear the triangle builds up with each extra face we add to the dice.
|
|
|
|
|
|
|
| (1, 1) |
(1,2) |
(2,2) |
(2,3) |
(3,3) |
(3,4) |
(4,4) |
| - |
(2,1) |
(1,3) |
(3,2) |
(2,4) |
(4,3) |
- |
| - |
- |
(3,1) |
(1,4) |
(4,2) |
- |
- |
| - |
- |
- |
(4,1) |
- |
- |
- |
The results for two 2 sided dice are embedded in the left 3 columns of table, then the results for two 3 sided dice on top of them, then two 4 sided dice. Each additional face will add 2 columns to the right. I'm not gonna formally prove anything, but hopefully it's obvious that it will always make a triangle.
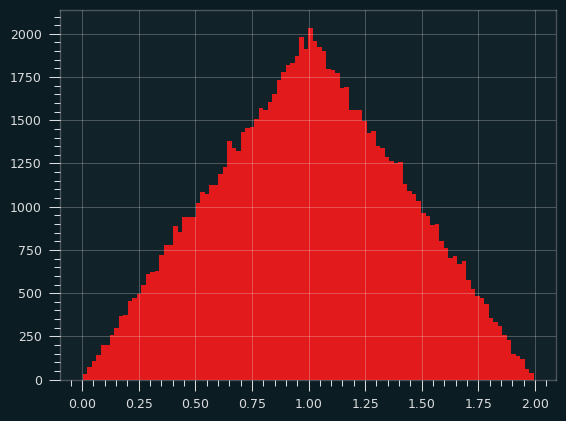
That's the triangular distribution.
Here's a simulation, calculating the sum of two random uniform variables over and over, and counting their frequencies:
3 is the magic number
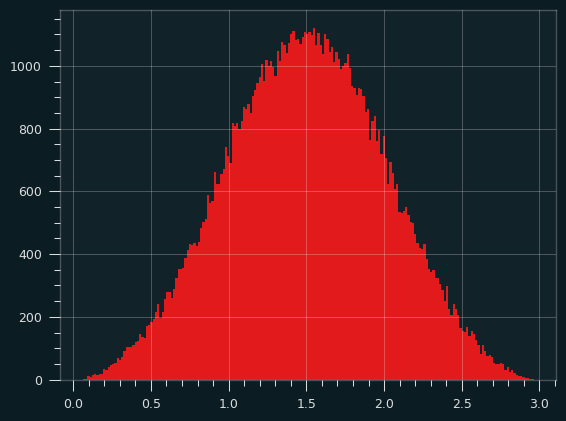
The sum (or average) of 3 Uniform random variables looks a whole lot like the normal distribution. The sides of the triangle round out, and we get something more like a bell curve. It's more than a parabola because the slope is changing on the sides. Here's what it looks like in simulation:
Here are three 4 sided dice. It's no longer going up and down by one step per column. The slope is changing as we go up and down the sides.
| 3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| (1, 1, 1) |
(2, 1, 1) |
(2, 2, 1) |
(2, 2, 2) |
(3, 3, 1) |
(3, 3, 2) |
(3, 3, 3) |
(4, 4, 2) |
(4, 4, 3) |
(4, 4, 4) |
| - |
(1, 2, 1) |
(2, 1, 2) |
(3, 2, 1) |
(3, 2, 2) |
(3, 2, 3) |
(4, 4, 1) |
(4, 3, 3) |
(4, 3, 4) |
- |
| - |
(1, 1, 2) |
(1, 2, 2) |
(3, 1, 2) |
(3, 1, 3) |
(2, 3, 3) |
(4, 3, 2) |
(4, 2, 4) |
(3, 4, 4) |
- |
| - |
- |
(3, 1, 1) |
(2, 3, 1) |
(2, 3, 2) |
(4, 3, 1) |
(4, 2, 3) |
(3, 4, 3) |
- |
- |
| - |
- |
(1, 3, 1) |
(2, 1, 3) |
(2, 2, 3) |
(4, 2, 2) |
(4, 1, 4) |
(3, 3, 4) |
- |
- |
| - |
- |
(1, 1, 3) |
(1, 3, 2) |
(1, 3, 3) |
(4, 1, 3) |
(3, 4, 2) |
(2, 4, 4) |
- |
- |
| - |
- |
- |
(1, 2, 3) |
(4, 2, 1) |
(3, 4, 1) |
(3, 2, 4) |
- |
- |
- |
| - |
- |
- |
(4, 1, 1) |
(4, 1, 2) |
(3, 1, 4) |
(2, 4, 3) |
- |
- |
- |
| - |
- |
- |
(1, 4, 1) |
(2, 4, 1) |
(2, 4, 2) |
(2, 3, 4) |
- |
- |
- |
| - |
- |
- |
(1, 1, 4) |
(2, 1, 4) |
(2, 2, 4) |
(1, 4, 4) |
- |
- |
- |
| - |
- |
- |
- |
(1, 4, 2) |
(1, 4, 3) |
- |
- |
- |
- |
| - |
- |
- |
- |
(1, 2, 4) |
(1, 3, 4) |
- |
- |
- |
- |
The notebook has a function to print it for any number of faces and dice. Go crazy if you like, but it quickly becomes illegible.
Here's the results of three 12 sided dice:
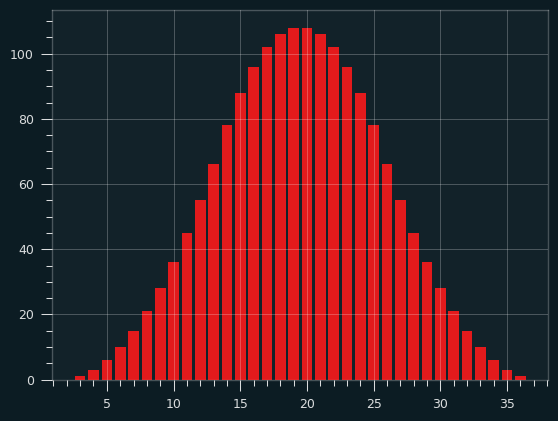
This isn't a Normal distribution, but it sure looks close to one.
Toast triangles
What if we feed the triangular distribution through the sin() function? To keep the toast analogy going, I guess we're spreading the butter with a sine wave pattern, but changing how hard we're pressing down on the knife to match the triangular distribution -- slow at first, then ramping up, then ramping down.
Turns out, if we take the sine of the sum of two uniform random variables (defined from the range of -pi to +pi), we'll get the arcsin distribution again! [2] I don't know if that's surprising or not, but there you go.
Knowing your limits
There's a problem with the toast analogy. (Well, at least one. There may be more, but I ate the evidence.)
The probability density function of the arcsine distribution looks like this:
It goes up to infinity at the edges!
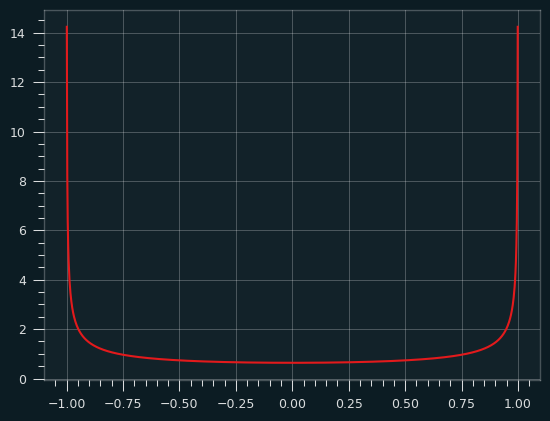
The derivative of the arcsin function is 1/sqrt(1-x**2) which goes to infinity as x approaches 0 or 1. That's what gives the arcsine distribution its shape. That also sort of breaks the toast analogy. Are we putting an infinite amount of butter on the bread for an infinetesimal amount of time at the ends of the bread? You can break your brain thinking about that, but you should feel confident that we put a finite amount of butter on the toast between any two intervals of time. We're always concerned with the defined amount of area underneath the PDF, not the value at a singular point.
Here's a histogram of the actual arcsine distribution -- 100,000 sample points put into 1,000 bins:
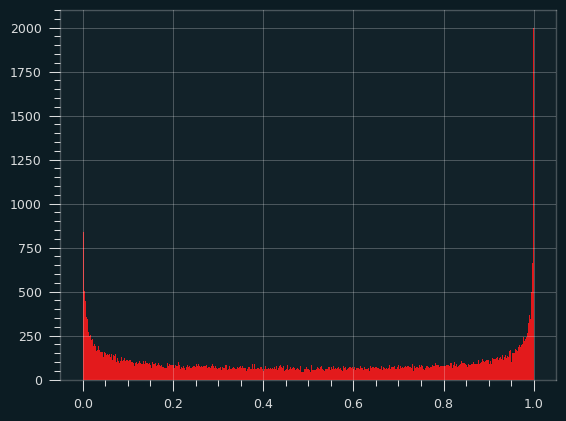
About 9% of the total probability is in the leftmost and rightmost 0.5% of the distribution, so the bins at the edges get really, really tall, but they're also really, really skinny. there's a bound on how big they can be.
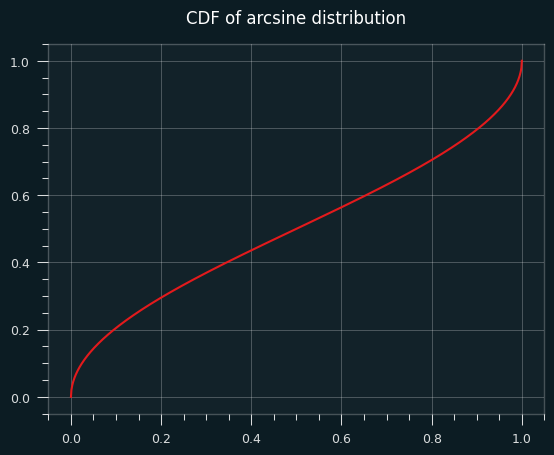
The CDF (area under the curve of the PDF) of the arcsine distribution is well behaved, but its slope goes to infinity at the very edges.
One for the road
The sinc() function is defined as sin(x)/x. It doesn't lead to a well-known distribution as far as I know, but it looks cool, like the logo of some aerospace company from the 1970's, so here you go:
Would I buy a Camaro with that painted on the hood? Yeah, probably.
An arcsine of things to come
The arcsine distribution is extremely important in the field of random walks. Say you flip a coin to decide whether to turn north or south every block. How far north or south of where you started will you end up? How many times will you cross the street you started on?
I showed with the hot hand research that our intuitions about randomness are bad. When it comes to random walks, I think we do even worse. Certain sensible things almost never happen, while weird things happen all the time, and the arcsine distribution explains a lot of that.
References/further reading
Jul 24, 2025
(This is an excerpt from a larger project about sports gambling. Code and early drafts of some of the materials can be found at https://github.com/csdurfee/book.)

I'll be talking about "the public" in this installment, by which I mean the side of a wager that gets the most number of bets placed on it.
I talk about the vig a lot without explaining it. It's explained in the book, but the short version is on standard bets, a gambler needs to win at least 52.4% of the time against the spread to break even due to needing to risk $110 to win $100. That $10 difference is the vig -- how the sportsbook makes their money.
In gambling circles, bets are often framed as Vegas or the sharps versus the public. Sharp started out as a term for cheaters -- dishonest bookies setting unfair lines, or card sharps who win thru deception rather than skill. The meaning has changed a bit over time. In modern parlance, a sharp is someone who wagers on sports as a game of skill, making money over the long term by placing bets with positive expected value. But the negative connotation persists in popular chatter about gambling. There's something unseemly about using math to decide which bets to take.
Say there's a game between the Lakers and the Charlotte Hornets, and the Hornets win against the spread. The public lost. What degenerate is betting the Hornets? Sharps, that's who. You'd think the public wouldn't have a problem with the sharps -- at least someone won money off Vegas tonight. Without the sharps, all the money that the public lost would go to Vegas. But Vegas and sharps are often conflated together. It's the public versus everybody.
It seems unlikely to me that it's always the public on one side of the bet and sharps on the other. The public is still right around 50% of the time, right? They can't be drastically worse than a coin flip, so taking the opposite bets can't be drastically better than a coin flip. That means that sharps are going to agree with the public at least some of the time. They might fade the public (bet the opposite side) more often than they agree with the public, but there's probably a fair amount of both.
How do bettors do against the spread as the season goes on?
Does the public side do better over time? If records against the spread were random and the lines totally fair, we'd expect the public's winning percentage to bounce around pretty close to 50%, spending about as much time on both sides of the line -- sometimes doing a little better than 50%, sometimes a little worse. Over the course of the season, the public's cumulative record against the spread should get closer and closer to 50%, as the sample variance gets smaller.
Here's the 2024-2025 data. This is the public's winning percentage, graphed as a 100 game moving average:
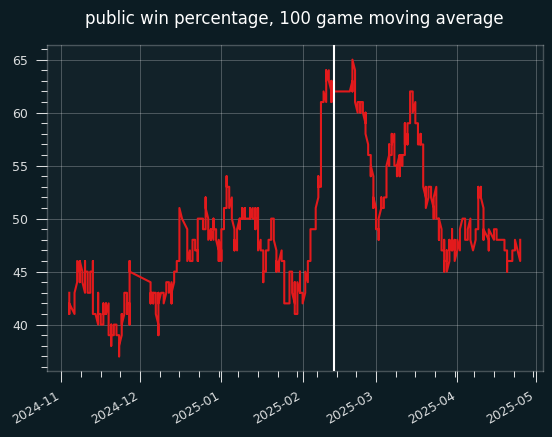
The white line is the start of the All-Star break. The public was winning well below 50% of their bets until a surge in the 100 or so games before the break, as we can see on the cumulative graph:
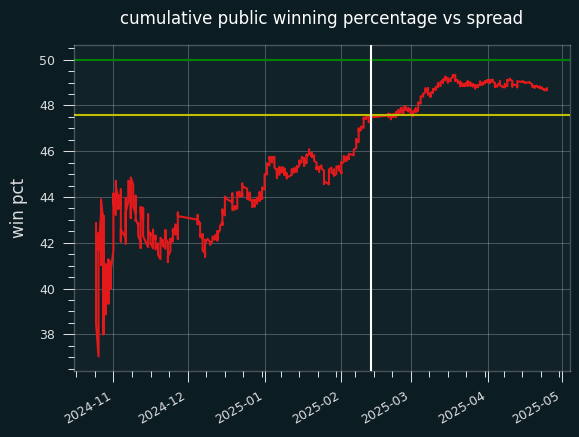
The public ended up going 584-614 on the season. Someone taking the public side of every bet against the closing line would have lost 91.4 units on the season, for a 48.75% winning percentage.
The yellow line is the break-even point for fading the public -- taking the non-public side on every bet over the season. Up until that surge before the All Star break, it would've been extremely profitable to do so. Even by the end of the year, the public's win percentage didn't get close to 50%. Someone betting at -105 reduced juice could have made .8 units by fading the public on every single bet.
The public were 369-388 when betting on the favorite, and 215-226 betting on the underdog. They went 293-311 when the away team won, and 291-303 when the home team won. They were bad no matter how you slice it.
While that's all super weird, it's only one season. My data source (sportsbookreview.com) only has spotty data for the 2023-24 NBA season, but they do have mostly complete data for 2021-22 and 2022-23. (Nothing before that, unfortunately.)
2021-22 season
I have data for 1108 out of 1230 regular season games for 2021-22.
The public went 566-542 on the season, for a loss of 30.2 units, much better than 2024-25.
Here's the 100 game moving average:
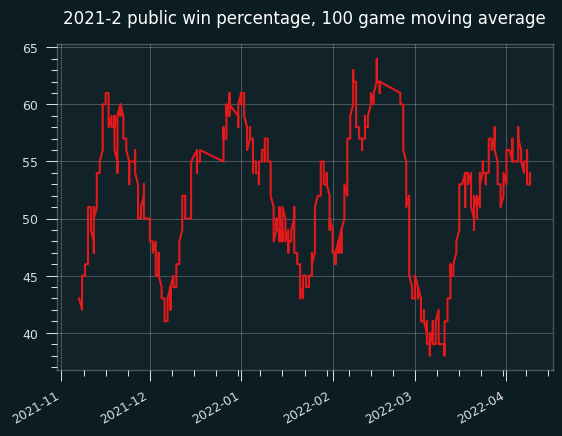
Except for a dip in early March, the public did consistently fairly well. Not well enough to make money, but better than 50% win percentage.
On the cumulative graph, while fading the public (yellow line) would have been profitable for the first month or so, the graph spends most of the season over the 50% line. However, it never gets over 52.4%.
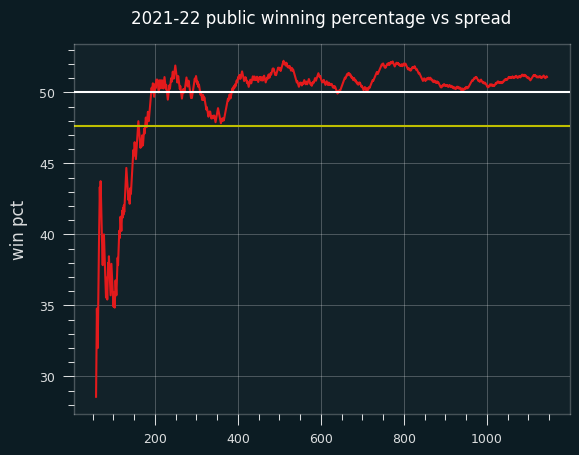
2022-23 season
I have data for 1176 off 1230 games in 2022-23.
The public went 587-589 for the season, for a loss of 61 units on the season. That's remarkably fair, if the vig weren't a factor. Here's the moving average:
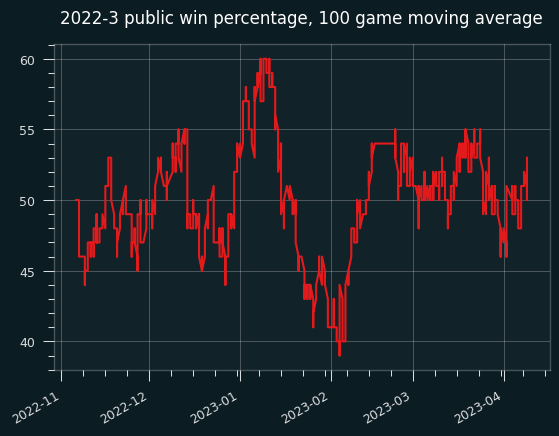
And the cumulative:
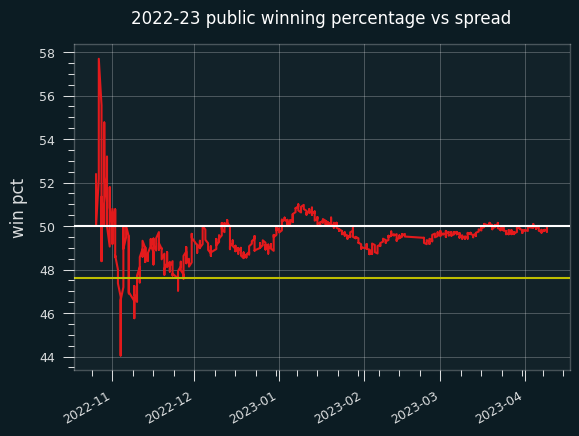
This one is similar to the 2023-24 graph, where the public pretty consistently lost a little bit more the 50% of the time, but not often enough to make fading the public a viable strategy.
Are team records against the spread random?
I started to answer this last time, but didn't have time to go deeper. If betting records are random, previous performance gives no information about future performance. Each game is like a coin flip, with equal chances of heads and tails. Teams will have good or bad records against the spread due to chance alone.
However, I gave some plausible reasons why this might not be the case.
The simplest way to test this I could think of was comparing records against the spread in the 1st half of the season to the 2nd half of the season. If the records are random, there should be no correlation between 1st half and 2nd half records.
I found there was a positive correlation between 1st half and 2nd half records in all three seasons I have data for. In 2023-24, the correlation coefficient was .10. In 2022-23, it was .40, and in 2021-22 it was .27. Only 2022-23 was statistically significant. Assuming randomness, positive and negative correlation should be equally likely. So all three being positive is suspicious. I don't think records against ths spread are totally random.
Say we track which teams had winning records against the spread over the 1st half of the season, then bet on those teams for the 2nd half of the season. (I didn't bother to filter out the games where teams with winning records play each other, so this analysis isn't perfect.)
In 2024-25, that would give a record of 297-297 ATS -- can't get more fair than that.
In 2022-23, it would have gone 279-241, for a profit of 13.9 units at standard vig, and a 53.7% winning percentage.
In 2021-22, it would have gone 247-225, for a loss of .5 units and a 52.3% winning percentage.
So, it's definitely not enough to be profitable as a strategy on its own. But it's close, and that's interesting.
A gambler needs to win at least 52.4% of the time to break even against the vig. Say they're picking from a subset of bets that have a 52.3% chance of winning, as the naive strategy achieved in 2021-22. They'd just barely need to do better than flipping a coin to be profitable. That could be much easier than picking from a set of bets with a 50% chance of winning, right?
Final thoughts
In all three seasons, the public did a little worse in the first half of the season than the second half. In the two most recent seasons, the cumulative winning percentage was below 50% for nearly the whole season.
That doesn't seem random to me. It makes sense that sportsbooks would offer slightly more favorable odds to the less popular team in order to attract equal money on both sides. It also makes sense that sportsbooks would be happy if the team with more money on it lost over 50% of the time. The difference between the public winning 50% of the time and the public winning 48.5% of the time could be significant on enough betting volume.
In all three seasons, there was a positive correlation between a team's record against the spread over the first half of the season and the second half. The correlation is strong enough that over 3 seasons, it's almost possible to make money by betting on teams with a good first half record.
On both points, I don't have nearly enough data to draw grand conclusions about how "the market" operates -- this is just one sportsbook, and an unknown one at that. Yahoo and DraftKings also provide betting percentage data, which would be useful for cross-checking these trends. I'm going to hold off for now, though -- there are too many other interesting things in the world.
Jul 18, 2025
code available at https://github.com/csdurfee/book.

Two types of people
Lots of sportsbooks publish info on how much action they've gotten on each side.
Here's DraftKings': https://dknetwork.draftkings.com/draftkings-sportsbook-betting-splits/
It's a smart move. It's good for SEO (to the extent that still matters). And I'm sure they get a lot of people who decide to take bets from that page.
For example, the Pacers were playing Brooklyn the night I wrote this. 27% of the bets were on Brooklyn at +10.5. 73% are on Pacers -10.5.
Somebody who sees that and decides to make a bet based on that information could bet either way. They could either tell themselves, "Everybody's taking the Pacers, so it must be a good bet" or "Everybody's taking the Pacers, so it must be a bad bet".
What are those two groups like when they're not betting on basketball, do you think? Do they use the same kind of toothpaste? Watch the same kind of TV shows? Vote the same way?
The public gets what the public wants
One bit of gambling lore is that there are "public" teams that get bet on more frequently, regardless of the line. Like, your cousin who's a Cowboys fan is going to bet the Cowboys on Thanksgiving regardless of whether it's a fair line or not. He'd watch the game and root for the Cowboys anyway, but it's a little more fun that way. The Cowboys aren't just a random number generator to him.
There's a social aspect to gambling now that I imagine didn't exist when it was underground. Lots of gamblers will follow bets that other people have placed. If the bet wins, I'm sure it's a cool communal thing to be a part of. But social media often doesn't obey the wisdom of crowds -- in places like reddit where users vote content up and down, the conventional wisdom is going to be amplified, and people with minority opinions are going to be suppressed. If well over 90% of sports gamblers lose money long term, the majority opinions are going to be bad.
I scraped betting percentage data from sportsbookreview (SBR) for the 2024-5 season. They don't say where they get the betting percentages from. If I had to guess, it would be MGM Grand, their primary source of other data. The SBR numbers seemed to indicate more action overall than a couple other sources I found -- the betting percentages were closer together. Other sites had games where there's 10% action on one side and 90% on the other, which seems implausible on a large volume of bets. So it's probably a pretty big site, whatever it is.
As with the data from the previous installment, there are 32 games out of 1230 missing data.
The money_percents column is the median amount bet on each team. The money_game_winners column tracks the number of games where that team got the majority of the money bet on their side. Both of these can be taken as indicators of how much teams are favored by the public.
Here are the teams sorted by money_percents. The teams near the top were less popular with gamblers, the teams at the bottom more popular.
|
winner |
loser |
ats_win_pct |
money_percents |
money_game_winners |
| New Orleans |
34 |
44 |
44 |
39.5 |
20 |
| Charlotte |
36 |
42 |
46 |
41.5 |
24 |
| Miami |
39 |
41 |
49 |
43 |
20 |
| Philadelphia |
26 |
52 |
33 |
43.5 |
29 |
| Portland |
45 |
33 |
58 |
43.5 |
25 |
| Orlando |
41 |
40 |
51 |
44 |
29 |
| Utah |
39 |
38 |
51 |
45 |
33 |
| Sacramento |
35 |
44 |
44 |
45 |
32 |
| L.A. Clippers |
47 |
34 |
58 |
46 |
27 |
| San Antonio |
38 |
41 |
48 |
47 |
31 |
| Chicago |
42 |
38 |
52 |
47 |
36 |
| New York |
38 |
44 |
46 |
48 |
38 |
| Phoenix |
29 |
49 |
37 |
48 |
36 |
| Washington |
33 |
46 |
42 |
49 |
37 |
| L.A. Lakers |
48 |
33 |
59 |
51 |
42 |
| Indiana |
38 |
43 |
47 |
51 |
42 |
| Atlanta |
37 |
42 |
47 |
52 |
41 |
| Boston |
39 |
42 |
48 |
52 |
43 |
| Minnesota |
37 |
43 |
46 |
52 |
43 |
| Dallas |
37 |
44 |
46 |
52 |
41 |
| Detroit |
41 |
38 |
52 |
53 |
43 |
| Brooklyn |
42 |
35 |
55 |
53 |
41 |
| Toronto |
49 |
28 |
64 |
53 |
47 |
| Golden State |
42 |
40 |
51 |
54 |
51 |
| Houston |
44 |
38 |
54 |
54 |
49 |
| Oklahoma City |
53 |
29 |
65 |
54.5 |
54 |
| Milwaukee |
44 |
38 |
54 |
56.5 |
56 |
| Cleveland |
47 |
33 |
59 |
57 |
53 |
| Memphis |
41 |
41 |
50 |
57 |
51 |
| Denver |
37 |
45 |
45 |
58.5 |
63 |
The public favorites
The most popular teams with NBA gamblers were Denver, Cleveland, Memphis, Milwaukee, and Oklahoma City. Denver got the most money in 63 of 82 games they played, which is remarkable.
Cleveland, OKC and Memphis were dominant for most of the season.
Denver and Milwaukee have two of the best and most entertaining players in the league. Both Giannis for Milwaukee and Jokic for Denver are fun to root for. People like to take bets on teams that are fun to follow.
The ugly dogs
The bottom teams were New Orleans, Charlotte, Miami, Philadelphia and Portland. All these teams except for Portland were total bummers to watch and cheer for this year. They had injuries and organizational dysfunction that led to totally wasted seasons. People don't like to take bets on teams that are a bummer to follow.
This hints at the fact that a lot of people are taking bets because they want that team to win the bet, rather than because they believe the bet has a positive expected value. It's entertainment, not a business investment.
Against the spread
Here's the same data sorted by record against the spread.
|
winner |
loser |
ats_win_pct |
money_percents |
| Philadelphia |
26 |
52 |
33 |
43.5 |
| Phoenix |
29 |
49 |
37 |
48 |
| Washington |
33 |
46 |
42 |
49 |
| New Orleans |
34 |
44 |
44 |
39.5 |
| Sacramento |
35 |
44 |
44 |
45 |
| Denver |
37 |
45 |
45 |
58.5 |
| Dallas |
37 |
44 |
46 |
52 |
| Charlotte |
36 |
42 |
46 |
41.5 |
| Minnesota |
37 |
43 |
46 |
52 |
| New York |
38 |
44 |
46 |
48 |
| Indiana |
38 |
43 |
47 |
51 |
| Atlanta |
37 |
42 |
47 |
52 |
| San Antonio |
38 |
41 |
48 |
47 |
| Boston |
39 |
42 |
48 |
52 |
| Miami |
39 |
41 |
49 |
43 |
| Memphis |
41 |
41 |
50 |
57 |
| Orlando |
41 |
40 |
51 |
44 |
| Utah |
39 |
38 |
51 |
45 |
| Golden State |
42 |
40 |
51 |
54 |
| Detroit |
41 |
38 |
52 |
53 |
| Chicago |
42 |
38 |
52 |
47 |
| Houston |
44 |
38 |
54 |
54 |
| Milwaukee |
44 |
38 |
54 |
56.5 |
| Brooklyn |
42 |
35 |
55 |
53 |
| L.A. Clippers |
47 |
34 |
58 |
46 |
| Portland |
45 |
33 |
58 |
43.5 |
| L.A. Lakers |
48 |
33 |
59 |
51 |
| Cleveland |
47 |
33 |
59 |
57 |
| Toronto |
49 |
28 |
64 |
53 |
| Oklahoma City |
53 |
29 |
65 |
54.5 |
Philadelphia, Washington and Phoenix were just as terrible at the sportsbook as they were on the basketball court. OKC and Cleveland had outstanding seasons in both places.
However, there's only a rough correlation between how good the teams were at actual basketball, and at beating the spread. Minnesota, New York and Denver were in the bottom 10 by winning % against the spread, even though they had good records and were doing their best to win. Denver lost to the eventual champs, and New York and Minnesota made the conference finals. Indiana was the 10th worst team against the spread, and made the NBA Finals. Toronto and Brooklyn weren't really trying to win a lot of basketball games, but ended up in the top 10. There is no good reason I can think of for the Lakers to be in the top 4 against the spread -- aren't they the epitome of a public team that should be getting unfavorable lines?
Which teams should the public love and hate?
I calculated the amount of units a gambler would win or lose if they bet on each team when they got the majority of the bets. This is a sort of measure how happy the proverbial public should be about each team.
public_units is the amount won/lost betting in favor of the team. Phoenix, Sacramento, Dallas, Denver and Indiana disappointed the public the most.
|
public_units |
| Phoenix |
-16.5 |
| Sacramento |
-14.2 |
| Dallas |
-13.6 |
| Denver |
-12.6 |
| Indiana |
-12.6 |
| Atlanta |
-11.5 |
| Utah |
-11.1 |
| Chicago |
-10.2 |
| Minnesota |
-9.5 |
| Detroit |
-7.4 |
| Philadelphia |
-6.7 |
| New York |
-6.1 |
| Brooklyn |
-5.2 |
| Washington |
-5 |
| Boston |
-3.2 |
| New Orleans |
-3.1 |
| Memphis |
-1.5 |
| Charlotte |
-1.2 |
| Miami |
-1 |
| San Antonio |
-0.5 |
| Orlando |
-0.4 |
| Milwaukee |
1.4 |
| Golden State |
2.7 |
| L.A. Lakers |
4.2 |
| Houston |
4.9 |
| Cleveland |
6.8 |
| Portland |
10.3 |
| Toronto |
11.3 |
| L.A. Clippers |
12.3 |
| Oklahoma City |
18.3 |
This is a pretty random list of teams, in both directions. It's a good illustration that gamblingball is different from basketball. It's not clear whether gamblingball is a game with an element of skill, or if it's all chance.
Are records against the spread due to chance?
If we assume that all variations are due to randomess, each game should be a coin flip whether the underdog or favorite wins against the spread.
Calculating exact odds using the binomial distribution, 94% of NBA teams should have between 33 and 49 wins against the spread over an 82 game season.
We'd expect 2 teams to be outside that range, and there are 3. Philadelphia went 26-52 in 78 games we have data for. Even if they won the other 4 games that are missing data, they'd only have 30 wins. So that record was definitely an outlier, but overall the season was about what we'd expect based on chance.
I find it very believable that some teams are more likely to have a winning record against the spread, because they are underestimated by the handicappers or the betting public. They end up getting lines that are too generous, and thus do better than expected against the spread over the long run. Toronto could be an example of that. They were bad, but they weren't really as bad as people thought.
Other teams could be inherently worse against the spread, as well. Perhaps they are super popular to bet on, so the lines tend to move against them -- a public team. Or perhaps gamblers and sportsbooks overvalue the team -- the conventional wisdom is that they'll be good when they're not. That definitely describes Philadelphia and Phoenix.
In both cases, the teams themselves aren't necessarily doing anything to be better or worse against the spread than an average team would be. It's about the perceptions of the bookmakers and gamblers. Teams can't help what bookmakers set the lines to be.
Do gamblers follow the record against the spread?
If a team's record against the spread is due solely to random error, then we've got a LeMartingale on our hands. The current record would have no bearing on the future record. So gamblers shouldn't factor it in when deciding to take a bet or not.
By the end of the season, there was a significant correlation between money percents and win percentage against the spread. I wanted to see how that might've changed over time. So I generated the table shown above for every single day of the season, and calculated the correlation on that day. Here's what that looks like over time:
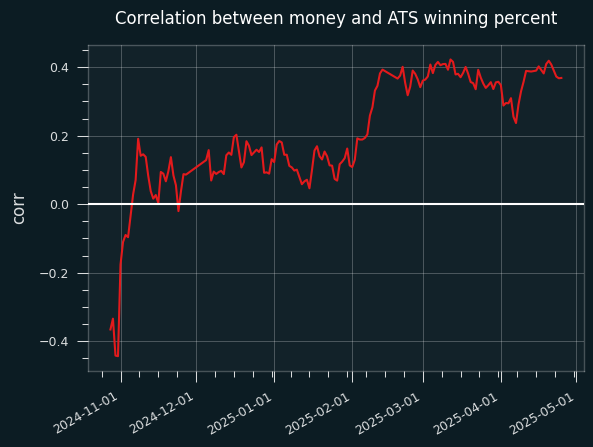
The money percentages are cumulative, the mean of all games in the season that have come before -- it's not showing gamblers' betting behavior on a particular day. The graph is a lot smoother that way, but we're losing something.
It also doesn't show whether records against the spread are a Martingale or not. The correlation between betting percentages and win records increases over time, but that doesn't mean this is because gamblers are behaving rationally.
The jump in correlation around mid-Februrary corresponds to the All-Star break, which is curious.
Stay tuned; I'll have more on this.
Jul 17, 2025
(This is an excerpt from a larger project about sports gambling. Code used, and early drafts of some of the chapters can be found at https://github.com/csdurfee/book.)

Efficiency of betting markets
The efficient market hypothesis says that given enough time and competition, free markets are able to establish the correct price for a commodity. In the case of sports betting, we could think of it as the price of a money line bet.
On a money line bet, you are betting on who will win the game straight up. You get a smaller payout for betting on the favorite, and a larger payout betting on the underdog. In the United States, money line bets are written in a goofy way. If the money line is negative, that's how much money you have to risk in order to win $100. For example, -200 indicates you have to risk $200 to win $100. If it is positive, that's how much money you win if you risk $100. If it sounds like a bad way to write the odds, you're correct.
A market maker will respond to an imbalance in bets by adjusting the price. If CLE -300 is a good value, people will rationally want to take it, driving the price up to, say -400. If it is a bad value, people will rationally want to take the other side and the price might go down to -200. These rational actors will collectively push the price towards the best possible estimate that humans can make given all information available at the time. It serves as a sort of collective intelligence.
In the first installment, I showed that humans are irrational when it comes to sports betting, so I was skeptical of how good, or fair, the lines could be. Could I find proof of this collective intelligence in action? Are there any obvious market inefficiencies?
The data & stuff to know
Stats are from the NBA season. I screen-scraped the data from sportsbookreview.com. All data is from the MGM Grand. Unfortunately, some data is missing around Christmas, and a few random days in between. 32 games are missing from the data set out of 1230 total, 2.6% of all games. These are games that don't appear on sportsbookreview's website, or have incomplete data on there.
This is an analysis of the MGM Grand's NBA lines for 2025. It's not a comprehensive guide to how the lines work.
There are always two lines on each game, one for the home team and one for the away team. Each side may have different vigs. Say for instance Bucks @ Pacers starts out at IND +3.5 -110/MIL -3.5 -110. It could close at IND +3.5 -115/MIL -3.5 -105. So it costs more to bet on the Pacers, but the actual line didn't move. I'm mostly ignoring that, but will point out when it's relevant.
"Line" and "spread" mean the same thing.
"Reduced juice" means risking -105 or -106 instead of the usual -110 to win 100. A "unit" is a gambler's standard betting size. "4.1 units of profit" would mean +$410 for a gambler betting $100 a game. Both are explained in much more detail in the book.
A note about pushes
When the final score agrees with the line exactly, neither side of the bet can be declared a winner. This is called a push. The bet is cancelled and everybody gets their money back. The casino makes nothing.
The MGM Grand always keeps point spreads on the half point (eg +6.5 or +7.5 rather than +7) so that they will never push. I don't think it's a bad policy, and I'm surprised more sportsbooks don't do it. The sportsbooks know how good their customers are at betting, so they should probably shade the point spread a half a point towards the side of the bet that has the less savvy bettors on it. (This assumes the sportsbook can identify and ban arbitrage gamblers, but more about that in the book.)
Analysis
If there is a wisdom of crowds, the final lines should be more accurate than the opening lines. Are they?
My code calculates the difference between the final score and the line, called the error. Because the MGM's lines always end in a half point, that means the error is going to be artificially high -- there will never be a game where it is exactly zero.
The opening and closing lines are a set of predictions. The smaller the difference between the line and reality, the better the prediction. Mean Squared Error is a standard way to compare two prediction systems in statistics and machine learning.
The MSE for the opening lines is 191.06, and the closing lines is 184.8. So we can say that in aggregate, the closing lines are more accurate than the opening lines.
MSE can't tell us how good the closing lines are, though, just that one set of predictions is better than another set. It's a relative measure, not an absolute one. We're squaring the error, so the MSE will always be positive. The errors in one direction don't cancel out ones in the other direction.
Let's look at how far the lines were off by. the Os are the opening lines, and X's are the closing lines. If the X is closer to the center line than the O, the market action made the line more accurate. I've plotted a random sample of 300 games to make the plot more readable.
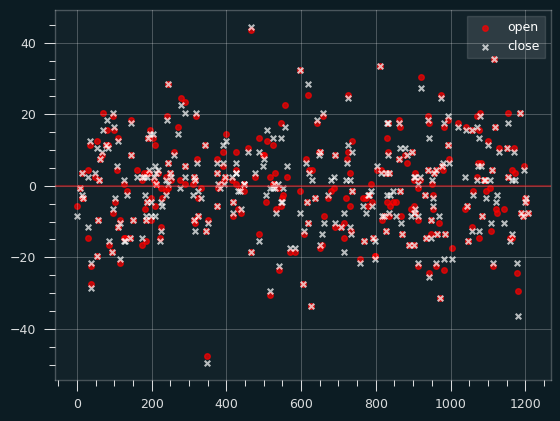
Unfortunately, that doesn't really show us much about how or when the closing lines are better than the opening ones.
Adam Smith, Handicapper
When were the closing lines more accurate than the opening lines?
The closing lines were better in 467 games, versus 384 games where the opening lines were better, and 347 games where the line never changed.
If the free market were a handicapper, and we interpreted the line movements as a bet on one side, they would have a 54.88% winning percentage (and 347 pushes).
While that's a respectable win percentage for a human trying to beat the spread, I was expecting better from the free market. The market only being right 55% of the time holds true for a couple of previous seasons I have looked at as well. NBA betting, as a market, is not very efficient.
There are good reasons for that. Sportsbooks that set the opening lines aren't trying that hard to be accurate. It's just a first guess. Only a tiny percentage of money is wagered at the opening line number. However, there are good reasons why lines tend not to move very much, even when the opening line is a bad one. For an in-depth explanation, check out The Logic of Sports Betting, by Miller and Davidow.
The myth of closing line value
The conventional wisdom is that sports betting markets are efficient, so that the only way to make money over the long run is by doing better than the closing lines, picking up on any flaws in the opening lines before the market eliminates them. Anyone else can only make a profit due to chance. From this perspective, the right way to measure a handicapper's skill is how their picks compare to the closing line. Say the opening line is Nuggets -3, and I take the bet at that number. The closing line is Nuggets -6. Then I captured 3 points of value against the closing line. This is known as closing line value (CLV). (We can figure out how valuable those 3 points are, and I show how in the book.)
Beating the closing line might be positively correlated with higher profits when analyzing betting records of touts -- people who sell betting picks for money. But when the market is wrong 45% of the time, focusing too much on CLV seems like a bad idea. There's no good reason to believe that a gambler is destined to lose money by picking against the closing lines. What if their strategy is to mostly bet against the prevailing wisdom on the 45% of games where the market is wrong?
CLV is a prime example of Goodhart's Law. As a measure of a handicapper's skill, it's probably fine (though not ideal). But it shouldn't be the target. A gambler shouldn't make picks explicitly to capture as much CLV as possible. That could be different on other sports. Football -- both forms of it -- attracts a lot more betting than the NBA does, so if you're looking for the wisdom of crowds, maybe look there.
Say the opening line is Nuggets -3 against the Timberwolves. I like the Nuggets in this matchup, but I think the public will go for the Timberwolves and it will finish at Nuggets -1/Timberwolves +1.
If I was trying to capture as much CLV as possible on this bet, I should take the Timberwolves +3 on the opening line, even though that's not the side I actually like!
If I was trying to actually win the bet, I should take the Nuggets at the closing line, hoping maybe I can get Nuggets -1 or even Nuggets +1. I can never get positive CLV on the Nuggets, because the market was wrong about them. Not me, the market!
CLV gets described as being the best way to test a handicapper's skill, but it's obviously non-optimal. Maybe it's the contrarian in me, but Opening Line Value -- identifying bets where the market is going to be wrong, and waiting till the last minute to place the bet -- is more impressive.
The best way to test a handicapper is to have them write out what they think the lines should be, rather than making a binary decision about somebody else's line (favorite or underdog). If a handicapper's lines are closer to the truth than the closing lines, they are good at handicapping. Looking at what bets they took is only a secondary signal of that. If they took Nuggets -7, is it because they thought the true line should be Nuggets -8, or Nuggets -12?
When the line doesn't move
Setting aside why the market moves in the wrong direction 45% of the time, I'm curious about the games where the spread didn't move at all. Maybe those lines were perfect as-is? If so, we'd expect to see equal splits of home vs. away winners, and underdog vs. favorite winners. There shouldn't be any bias to those games. The free market is essentially labelling these the pinnacle of the handicapper's art, impossible to be improved upon.
The difference between the predicted outcome (the line) and the actual outcome is a combination of how much the line maker got it wrong, plus random variation. So the games where the line didn't move should be totally random, right?
They're not. If we look at games where the line didn't move, the away team went 184-163 in those games. Someone betting the away team in every game where the line didn't move would win 53% of their bets, for 4.7 units of profit at full vig, or 11.2 units of profit at reduced juice.
There's also a bias towards underdogs, who went 186-161 in this situation. Always taking the underdog would give a 53.6% winning percentage, for 8.9 units at full vig, or 15.3 units at reduced juice.
There's an even bigger bias if we combine the two. Away underdogs went 122-92 in these games, which is a 55.2% winning percentage, for 13.1 units of profit at full vig, and 17.1 at reduced juice.
None of these results are statistically significant, but they are very :thinking_face_emoji:
About the vig
When the vig is imbalanced, the side with the higher vig should be more likely to win, because they're winning less money in return. Moving the vig from -110 to -115 is a way for the bookmaker to discourage bets on one side without moving the line. Likewise moving it to -105 is a way to encourage bets on that side.
Since the MGM Grand always keeps their lines on the half point, we'd expect them to adjust the vig often rather than change the spread. They do for most of the games where they didn't move the lines, but 39% of the time the vig stays at -110.
If we break down the games where the line didn't move by vig, the underdogs went 62-43 when the vig was high (-115), 74-62 when the vig was at the standard level (-110), and 50-56 at low vig (-105).
Someone taking the underdogs when the line doesn't move, and the vig is -110 or -115, would've gone 136-105 this season, a 56.4% winning percentage, and around 18 units of profit (factoring in the additional -115 vig on some bets).
Now, the strategy is pretty convoluted, and I wouldn't bet on it holding for future seasons, but it's definitely evidence there could be irrational factors at work in the market. It certainly doesn't show the market to be the well oiled machine that Closing Line Value assumes it is.
Must love dogs
Winners ended up being pretty evenly divided between favorites and underdogs by the end of the season, but underdogs were way ahead for most of the year.
Betting every single underdog against the spread over the first quarter of the season would've been fairly profitable -- a 165-136 record (54.8% winning percentage), and 15.4 units profit at full vig. People betting favorites got killed at the beginning of the season.
Dogs and favorites were basically even through the middle half of the season, before favorites finished off 167-144 (53.7% win percentage) to even things out.
Here's a plot of the winning percentage of favorites over the course of the season. I skipped the first 50 games because of noise. The yellow line represents the winning percentage necessary for betting all underdogs to be profitable (at standard vig). That happens when the favorites win less than 47.6% of the time (which means underdogs win more than 52.4% of the time.)
It wasn't until the last month of the season that blindly betting all underdogs started being a losing proposition, even factoring in the vig.
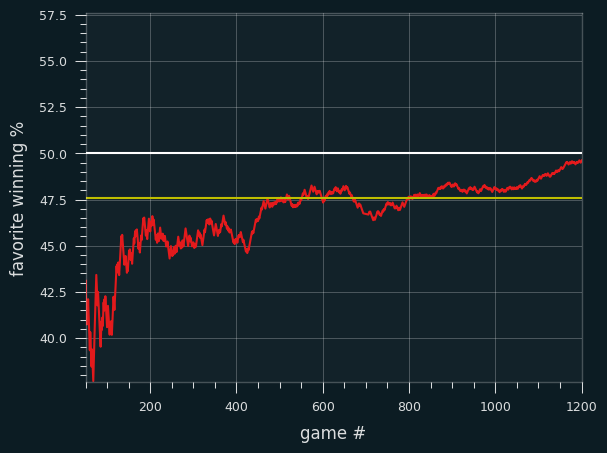
Did the lines improve over time?
I was curious if there was evidence that the errors were getting smaller, or more predictable over time.
The raw errors are too noisy to see any sort of pattern:
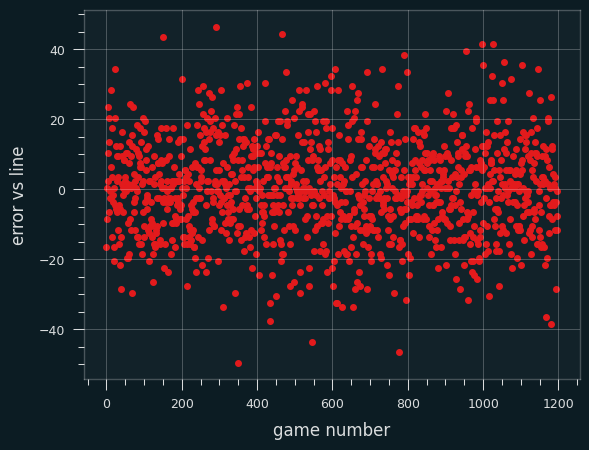
This is a plot of the 100 game moving average of the absolute error of the closing line. I don't see any trends to suggest the lines got more accurate with time.
The size of the error against the closing line isn't the ideal metric, because not all points are created equal -- the higher the line, the less surprising the error. (I'm going to skip discussing that for now, but it's explained in the book.)
Did the lines change over time?
I wondered whether the size of the lines changed over time -- did the games get more or less competitive over the course of the season?
This is a 100 game moving average of the average size of the spread. As we can see, the lines did get bigger near the end of the year.
It's possible the trend is due to scheduling, but the change at the end seems significant -- teams tend to give up near the end of the year. Bad teams want to be as bad as possible in order to get the best odds in the NBA draft, so they're not that competitive.
(I have a lot more to say about tanking, but I'll stay off my soapbox for now.)
What type of games are affected by line movement?
There were 130 games where the winner flipped from the favorite to the underdog, or the underdog to the favorite, because of the line movement. In other words, these are games where either side could have won the bet, depending on whether you took the opening line or the closing line.
These games were perfectly balanced -- 65 times, the favorite won (vs the closing line); 65 times the underdog won.
What about games where the spread was extremely accurate (off by 3 points or less)? Underdogs went 138-121 in those games (53.2%).
The difference is more dramatic in games where the line was off by 1 point or less. The underdogs went 56-33 (63% win percentage). Of course, there's no way to use that as a betting strategy since we can't identify these games before the fact, but it does show a small potential bias in favor of underdogs.
What would "perfect" lines even look like?
It's rare to see NBA lines that are bigger than +15/-15 points. There were 15 this season, about 4.4% of all games. That's around one NBA game a week with a line that high.
By contrast, 31% of NBA games end with a score differential of over 15 points. That's 7x more often, roughly one game a day.
The lines really shouldn't be as large as the final score differential, because they are an estimate of the mean outcome of the game. If the Celtics beat the Raptors by 54 points, that doesn't mean the line should have been Celtics -54. The Celtics and Raptors played 4 times last season (data taken from basketball-reference). I'm going to ignore home court advantage -- imagine these are played at a neutral gym. The first game, Boston won by 3. The second, Boston won by 54. The third game, the Raptors won by 13. The last game, Boston won by 10.
Boston won by an average of 13.5 points, so BOS -13.5 would be a reasonable line for all four games, as that's the best estimate we can make of their difference in skill. Only 1 of the 4 games ended up close to that line. For the other 3 games, the error was at least 10 points. That's pretty typical for NBA games. The error is usually around 10 points.
In this scenario, Boston -- despite being the much better team -- would have gone 1-3 against the spread. If the line for all four games was BOS -9.5, they would have gone 2-2, but the error would still be 44.5 points on the second game, and 23.5 on the third one.
The actual outcomes might be all over the place, but the spread isn't meant to predict the actual outcome, just the point where both sides are equally likely to win the bet. In a small sample size, there's no guarantee both sides will win 50% of the games, even if the line was perfect.
Here's a histogram of the spreads (for the away team) overlaid on a histogram of the errors against the spread:
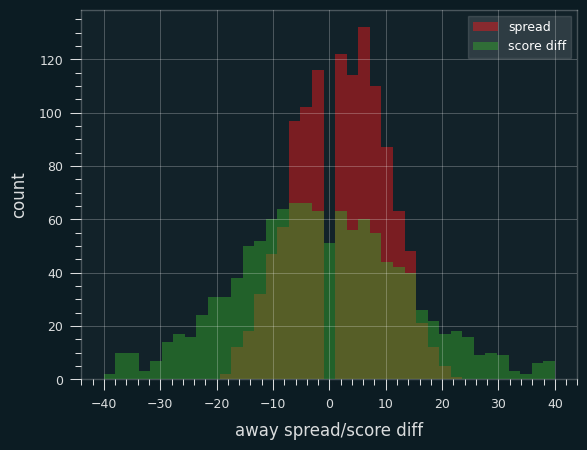
If we look at just the score differential, we can stick a bell curve over the top and it looks pretty normal:
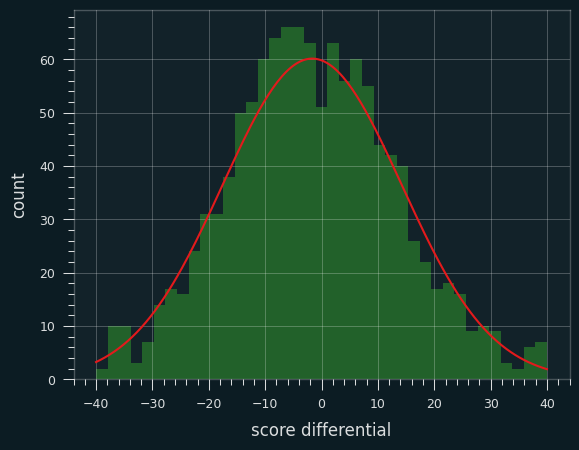
Simulating games from the spreads
The problem is, these aren't outcomes from one distribution. Every game is essentially a sample from a different distribution. Each game has a different mean (the spread, or rather the ideal version of it) and a different variance (how predictable games are between the two teams). Combining them all together, the results end up looking kinda normal (because a lot of things do).
I decided to simulate the entire season to show how the point differentials are going to be much bigger than the original lines.
I simulated every game by sampling from a normal distribution with the mean set to that game's spread, and the variance equal to the sample variance of all games that season with that spread.
Here's how they match up:
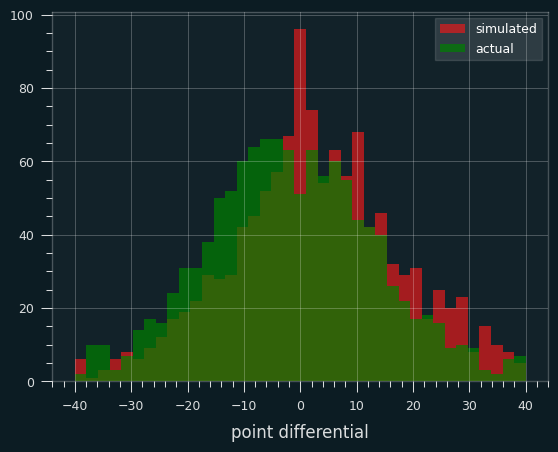
I know that's a pretty rough simulation. There's some weirdness in the middle. NBA games never end in a tie, and they end in a one point difference less often than expected due to tactical reasons, so there's a little notch right in the center of the green curve. If a team is down one, they foul the other team and hope they miss at least one of their free throws. There's also more simulated games than I would expect that end with a differential of +1 or -1. There very well may be a bug in my code. So there's a muddle in the middle. But the spread of the data is the same, which is the main point.
Hopefully the simulation shows that the lines shouldn't be bigger than they are, even though they are frequently off by many multiples compared to the final result. An error of 10 is about what we'd expect on average, and big errors don't necessarily mean Vegas was wrong. If the line is Dallas -3 and the other team wins by 27, that doesn't mean the line was off by 30 points. The line is meant to be an estimate of the mean outcome, if the teams played each other a large number of time under the exact same conditions. We only ever see one sample, though, and a lot of times it is far from the mean.
Jul 16, 2025
Code at https://github.com/csdurfee/book
Sportsbooks have many ways of encouraging people to lose their money as quickly and efficiently as possible. One of the best ways to do this is a type of bet called the parlay. "Parlez" means "to talk" in French, so it's no surprise dudes always want to talk about them online.
The idea behind a parlay is that you can bet on multiple events at once and if they all win, you make a nice profit, otherwise you lose. On a technical level, if the first bet on the parlay wins, the winnings are immediately placed on the second bet in the parlay, if that wins, it rolls over to the third bet, and so on. It's a sequence of bets, with the stakes going up with each bet. The individual bets in the parlay are known as "legs".
I'm going to keep asking this question: why would they be offering this bet if it was good for you? Parlays might be more fun, but that just means they found a way to get you to part with your money easier, which sounds like a bad thing.
We can compare different bets by using Expected Value (EV). EV is the weighted average of all the possible outcomes. If the expected value is positive, we will make money over the long run; if it's negative, we will lose money.
The traditional payout on a 4 team parlay is 10:1. What is the expected value of such a play? is it higher or lower than taking the individual bets?
It's easy to grind the math on this one, and see which option is better. I can't say "make us more money" because both types of bets are guaranteed losers without some sort of edge.
Parlays are such a bad type of bet on the surface that to understand them, I have to give a little taste of parlay culture first.
Nephew Doug
Say you want to place some bets. You just learned about betting on sports, so as a newbie you're trying to learn from experts by listening to gambling podcasts. These guys have been gambling for decades. Surely they must know what's up. Their wisdom will give you the edge for sure. Surely they will keep you from making costly mistakes.
You've listened to Nephew Doug's podcast, and wrote down his Locks of the Week. You're ready to enter them into your betting app, which has been hand-optimized to be as much of a dopamine and money sink as possible.
Because you listen every week, you know Nephew Doug has been burdened by the Gods with the gift of prophecy. Just ask him. He's like a modern day Cassandra, only it's about how the Cowboys are always going to suck.
Now, the Gods like a little competition. The Olympics were invented as a religious ceremony in their honor, after all. But they're not above making a call from on high to nudge the result a little bit. Yes, Zeus is definitely a Chiefs fan.
So you believe ahead of time Nephew Doug's picks will win 55% of the time. Which way of betting these picks will bring you the most money in the long run?
1) "throw 'em all in a 4 team parlay" like Doug and his buddy Jorts Guy do
2) randomly choose 3 of Nephew Doug's picks and bet them individually. Don't do anything with the 4th one.
Maybe option 2 seems insane to you. But let's game it out.
You listen to Nephew Doug, but I don't. My assumption would be this guy is no better than a coin flip -- he only wins 50% of the time, or close to it. Parlays at old school casinos pay at 10:1 and online sportsbooks pay 12.28:1. Let's see how that works out at 10:1 payout, the ones Jorts Guy and Nephew Doug were cutting their teeth on back in the day.
There are two ways to do the comparison. We could bet $100 on the parlay, and compare to putting $25 on each leg. Or we could compare $100 on the parlay to $100 on each leg.
Neither way of comparing is entirely fair, though, because the stakes increase throughout each leg of the parlay. If a gambler bets $100 on a 4 team parlay, they're risking $100 on the first leg. Assuming they keep winning, they're risking $190 on the 2nd leg, $300ish dollars on the 3rd leg, and $600ish dollars on the 4th leg.
For each leg of the parlay, the gambler should consider the risk of losing out on $600 if they took a 3 team parlay and it won. Risking $100 on the 4 leg parlay is sort of like taking 4 different $600 bets, because each one could cost the gambler that much if it loses.
I will be comparing risking $100 on the parlay versus $25 on each of the legs.
7x worse
This difference only matters for bettors with a high degree of skill. For the beginner, who we can reasonably assume will no better than a coin flip, the parlay is always a worse option. Almost 7 times worse. The parlays lose about 30% per bet, versus 4.5% for the straight bets.
Yikes. Maybe parlays are fun, but it's like blowing the whole week's vig budget on Sunday when compared to taking one regular bet a day.
Even a stretch of good luck is going to get swallowed up real fast if you're losing 30% of the stake on average. These types of parlays are a sadness machine.
Partially blessed
What if Nephew Doug truly has been partially blessed by the Gods, and can beat the lines 55% of the time? That's pretty good. Only a small percentage of sports bettors can achieve that, in my research.
The gambler should turn a profit either way, but maybe parlays offer a better return?
The parlays have an expected return of +0.66%, versus +5% for the straight bets. The straight bets make 7.6x as much money.
OK, what about if we just don't play the 4th bet? We will bet on the first three legs, and don't play the 4th one. We put the $25 for the fourth bet in our piggy bank and earn a 0% interest rate.
We're throwing out a bet with positive expected value, and risking angering the Gods by ignoring their chosen sports prophet, Nephew Doug. Perhaps that will tilt things in the parlay's favor.
Nope! The straight bets have a return of +3.75%, which is still 5.7x better than the parlays.
Finally, let's say we flip a coin to decide the 4th bet. It will only win 50% of the time, which means it's a guaranteed loser because of the vig -- you win less than you have to risk. (There is much more about the vig in the book.)
Nope! The coin flip hurts our profitability, but we're still clearing +2.6%, which is 4x better than the parlays. We'd have to do 2 of 4 bets by coin flip for the parlays to be more profitable.
To be fair, 55% is just barely profitable for an old-school parlay. The profitability increases exponentially as the win rate goes up. There is a win rate where parlays would make more money than the straight bets. If you win 100% of the time, the parlay is definitely a better deal, right? 10x profits taking the parlay versus 4x taking the original bets.
Successful handicappers who sell their picks on the internet are only winning around 55% of the time. If you have to do as well at something as people who do it for a living just to break even, that's not a great plan.
Online Parlays
Online 4 leg parlays pay out $1228 per $100 risked, which make them a little less bad. However, they're still way worse for the average gambler than taking the straight bets. At a 50% win rate, online parlays have an expected return of -17%, versus -4.5% for the straight bets. So they're 3.7x worse. They're half as bad as the old school parlays, but still terrible.
That $1228.33 payout for online parlays was chosen deliberately. It means that online parlays have the same break-even point as the individual bets (at standard vig) -- winning 52.4% of the individual bets. Because parlay profits climb exponentially, that means a skilled bettor with a 55% win rate will have a much higher EV with the parlays. They will have a +21.6% rate of return, versus +5%.
EV doesn't describe the range of outcomes
Expected Value is a good way of determining whether you can make money taking a certain type of bet, but it doesn't describe the range of possible outcomes. With parlays, a lot of those outcomes are bad, even for a gambler with enough skill to make them more profitable on paper.
Simulations are great in this sort of situation, because they can convey the range of possible outcomes in a way EV can't. I simulated 200 individual bets versus 50 parlays, and ran that 10,000 times. Our virtual gambler wins 55% of the time, and bets $100 on parlays, $25 on each individual bet.
The individual bets made more money (or lost less money) than the parlays 38% of the time. Just because the expected value is higher for the parlays, that doesn't mean they will always be more profitable.
More concerningly, the parlays had big losses (down more than $1000 on $100 bets) 33% of the time. That only happened 0.2% of the time on the straight bets. There were almost no small losses with the parlays, because the payout is so high and the number of bets (50 parlays) is so low. Winning one more parlay could be the difference between being down $1000, and breaking even.
Expected Value can't be the only thing we consider, because we don't live an infinite life. Our whole life is a small sample size, if the variance is high enough. Our bankrolls are always finite. The fact that we might make more money over 100 years is undercut by the fact that we'll die or go broke before then.
Even for the skilled bettor, parlays make it more of a game of luck. Let's say my simulation represents an entire season of betting on basketball. Imagine playing the parlays with a 55% win rate, being better than almost everybody at handicapping, and still having massive losses one season in three? When you'd make more money taking the individual bets 40% of the time, and only have a 1 in 500 chance of bad losses?
Parlay psychology
There's a weird psychology to the parlay as well. Even if you played every day, these parlays only win once every couple of weeks, so they'd be kind of a grim strategy in practice. A good bettor taking the individual bets will have winning days over half the time. Is it better to feel like a winner most days, or every other week?
Most people don't have to consider that question, though. Without a huge amount of skill at betting, the only scenario where they might make sense is as a lottery: something that can deliver a tiny chance of massive payouts without any skill.
What happens if we do the same simulation, but the win rate is 50%, like a coin flip, or most sports bettors? The parlays make money 38% of the time! Taking 200 straight bets will only make money 26% of the time. Isn't that a little surprising? Even though the straight bets have better expected value (well, less bad), they also offer less of an opportunity to make money based on chance alone.
What about over a longer time frame? I simulated 500 parlays versus 2,000 straight bets by flipping a coin. The parlays make money 12% of the time, versus only 1.74% of the time for the straight bets. However, the losses are much, much bigger than the wins:
12% is 1 in 8, which isn't that rare. 500 parlays could end up stretching over multiple seasons, perhaps a lifetime of sports betting. That means somebody who was making picks by flipping a coin could end up looking like a pretty good bettor for a long stretch if they are taking parlays. Of course, 88% of people will lose money, far more money than the 12% of profitable bettors win. In practical terms, it's like a lottery where you have a 12% chance of winning $3617, but an 88% chance of losing $10,221. Sound like fun?
It's really, really hard to tell if someone taking bets at long odds is actually good at betting, not without thousands of documented bets. Over 50 parlays, or even 500, it's not that surprising for some people to look smart on parlays by chance alone. It would be much better to assess their skill based on the individual bets they took within the parlays.
Other parlays
Parlays with only 2 or 3 legs have higher relative payouts compared to 4 leg parlays, so they're not nearly as bad. They'll also have less variance in outcomes than the 4+ leggers. I'll leave those calculations to the reader, though. While they're one of the least bad bets offered by the average sportsbook, it's extremely rare to see people talking about 2 or 3 leg parlays online. Gamblers love the higher payouts and drama of parlays with a bunch of legs. I will have a lot more to say about how people actually play the parlays in a future installment.
Same Game Parlays (SGPs) are a new type of bet which allows the player to make multiple wagers on the same game. For instance, someone could bet on their favorite team winning and their favorite player scoring over a certain amount of points and the guy they hate on the other team scoring under a certain amount of points, with a big payout if all 3 things happen. SGPs have become the most popular type of bet I see online, and deserve their own lengthy discussion. For now just think of them as the vape pens of betting. They're obviously super addictive, extremely popular with younger people, and you can't really know what's in them, but it's probably bad.
Gambling gurus, and the people who listen to them
I've taken up lot of hobbies over the years. It seems like every time I take up a new hobby, I end up spending a lot of money on stupid stuff at the beginning. Then I get into it more, and realize what matters.
There is an adverse selection process, where people who are new to a hobby have no idea what's actually good, what they actually need, or what things should actually cost. Filled with zeal to get started, they end up overpaying for inferior goods. Same thing for travelling in a new country. The guys at the train station trying to hustle you into a taxi are definitely not hooking you up with the cheapest way to get around.
Betting experts, the kind who have podcasts and big followings on social media, are supposed to know more about this stuff than the average person. They're supposed to be like the guidebooks, or the seasoned traveller telling the newbie to walk 2 blocks and take the metro for $2 instead of paying $100 for a taxi. Yet they're pushing parlays and other sucker bets, and pushing sportsbooks that charge full vig and ban anybody who wins too much. The "experts" are pushing beginners into bad situations. They're the creeps at the train station hustling naive tourists into their buddy's taxi.
Most of these experts don't do any better than flipping a coin, so I doubt they're actually making money on their "can't miss locks of the week". Gambling ads, sure. Everybody's taking gambling money right now, regardless of how it will hurt their brand, their audience, and sports long term. Clearly there's a lot of money in talking about it. That gambling money is there because these self-styled experts bring the sportsbooks more customers -- losing customers, specifically.
Where's all that ad money coming from? The sportsbooks wouldn't be throwing money at influencers who were actually winning consistently. Any gambling show they sponsor is pretty much guaranteed to lose you money, or it wouldn't be sponsored. Any bet they're promoting heavily, like they do with parlays, is because it makes them more money that way. You shouldn't need to know any math to figure out why they're pushing teasers and parlays and "profit boosters". I love that last one. It's like saying Idi Amin served mankind. Why would they care about boosting YOUR profits?
Unlike gamblers, sportsbooks don't make negative expected value plays due to emotions or lack of information. Your irrationality is their entire business.
Jul 12, 2025
Earlier this year, I wrote most of a book about the psychology and mathematics of sports gambling called Your Parlay Sucks. The book never quite came together, and is probably too weird to ever get published, but it has some interesting bits, so I figured I'd share them here.
Why did I get interested enough in sports betting to write a whole book about it? I think it's because I'm fascinated by the limits of rationality. Philosophers, economists and social scientists would like to treat humans as though they are capable of making rational decisions. That conflicts with the real world, where even pretty smart people make irrational choices. I certainly have.
Sports betting is a sort of rationality lab. You and I might have different values or beliefs. What's crazy to me might be normal to you, or vice versa, but we should both be able to agree that placing bets that are guaranteed to lose money is irrational.
This paper, "Intuitive Biases in Choice versus Estimation", is a wonderful illustration of cognitive bias and irrationality in the realm of sports betting.
The researchers had people bet on NFL football against the point spread. If you're not familiar, the idea behind the point spread is to attract an equal amount of action on both sides of the bet by handicapping one of the teams. If you bet on the favorite, they need to win by at least the amount of the spread for the bet to win. The other side side wins if the team loses by less than the spread, or wins the game outright.
Gamblers can bet either side, and if there are more bets on one side than the other, the sportsbook can change the spread to attract equal action. So there's a potential for the wisdom of crowds to kick in, the invisible hand of the market moving the line towards the best estimate possible.
Of course, that depends on gamblers being rational. A rational gambler has to be willing to take either side of a bet (or not bet at all), depending on the spread. If the spread is biased towards the underdog, they should be willing to take the underdog. If it's biased towards the favorite, they should take the favorite. And if the line is perfectly fair, they shouldn't bet at all.
As I showed a while back with ensemble learning, the wisdom of crowds only works if the errors that people make are uncorrelated with each other. If most people are wrong about a particular thing, the "wisdom of crowds" will be wrong, too.
This study found that people are consistently irrational when it comes to point spreads. They will tend to bet the favorite, even though both sides should have an equal chance of winning. It's probably easier to focus on which team is better, and assume that the better team is more likely to win against the point spread as well. It's harder to imagine the underdog losing the game but winning the bet, or pulling an upset and winning outright.
The study took things further and adjusted the lines to be biased against the favorite team, so that taking the favorite would be guaranteed to lose more than 50% of the time. They even told the gamblers that they did this. And the gamblers still overwhelmingly picked the favorites. The researchers continued the study for the whole season. Even after weeks and weeks of steadily losing, being told over and over that the lines are unfair, the gamblers still preferred to take the favorites. They never learned. The participants got to keep their winnings, so they had an incentive to be right. And they still couldn't do it.
Sportsbooks have a lot of ways of trick people into taking extra bad bets, as I will show. But they don't really need to. People will consistently take bad bets even if they should know they're bad bets.
Jun 30, 2025
(Notebooks and other code available at: https://github.com/csdurfee/hot_hand.)
Last time, we found that there are many players like LeBron, where their FG% is higher when they've missed most of their last 5 shots than when they've made most of them. However, most players don't have enough attempts when they've gone 0 or 5 out of their last 5 for a good statistical analysis.
So instead I will be looking at a binary split -- I will call a player cold when they've made 0, 1 or 2 of their last 5 shots, and hot when they've made 3, 4 or 5 of their last 5. Most players have a FG% between 40 and 60%, so this nicely splits them into times when they're shooting better than average versus worse than average.
Anthony Edwards
Anthony Edwards ("Ant") is particularly unstreaky for a young player. He's only completed 5 seasons in the league, but has the 5th biggest z score of the last 20 years. He could definitely catch LeBron someday.
Ant has the LeBron-like pattern of FG% trending downward when he's hot. He doesn't have anywhere near the volume of LeBron, so the spike at 20% (1/5) might just be noise. But overall, he shoots worse when he's been shooting well.
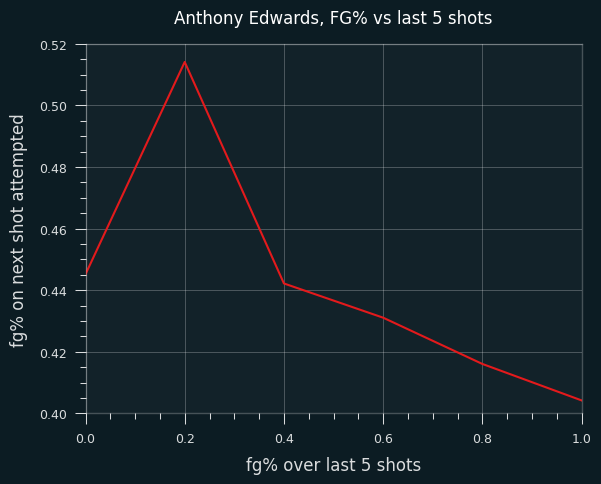
The trend appears to be due to shot selection. He takes far more above the break 3 pointers when he's hot than when he's cold. The additional 3 point attempts come at the expense of shots in the restricted area.
Here are the changes in tendencies:
| BASIC_ZONE | hot | cold | diff |
|:----------------------|------:|-------:|-------:|
| Above the Break 3 | 41.5 | 31.7 | 9.8 |
| Corner 3 | 3.6 | 4.8 | -1.2 |
| In The Paint (Non-RA) | 13.4 | 14.6 | -1.1 |
| Mid-Range | 14.1 | 12.2 | 1.9 |
| Restricted Area | 27.4 | 36.7 | -9.4 |
Of course, this would be justified if Ant shot above the break 3's better when he's hot, but he doesn't. He makes 37% of his above the break 3's when he's cold but that drops to 34% when he's hot. So he's trading restricted area shots, with an expected value of .601 * 2 = 1.202 points, for above the break 3's, with an expected value of .34 * 3 = 1.02 points.
Here are the changes in FG percentages. His FG% on corner 3's goes up, but it's on insignificant volume:
| BASIC_ZONE | hot | cold | diff |
|:----------------------|------:|-------:|-------:|
| Above the Break 3 | 34 | 37.1 | -3.1 |
| Corner 3 | 45 | 33 | 12 |
| In The Paint (Non-RA) | 40.8 | 34 | 6.8 |
| Mid-Range | 36.3 | 34.8 | 1.5 |
| Restricted Area | 60.1 | 65.4 | -5.2 |
The rest of the league
I looked at league-wide shot selection in hot/cold situations. I restricted to the last 10 seasons, since the rise of the 3 pointer has dramatically changed shot selection. Here are changes in shot selection for all players:
| BASIC_ZONE | hot | cold | diff |
|:----------------------|------:|-------:|-------:|
| Above the Break 3 | 22.1 | 22.3 | -0.2 |
| Corner 3 | 6.2 | 7 | -0.9 |
| In The Paint (Non-RA) | 15.8 | 15.3 | 0.4 |
| Mid-Range | 25.3 | 23.5 | 1.8 |
| Restricted Area | 30.7 | 31.8 | -1.2 |
The mid-range shot is the lowest value shot type, so it's notable that the rate goes up when players are hot. These additional mid ranges come at the expense of Corner 3's and Restricted Area shots, the two most valuable types of shots.
As before, changes in shot selection could be justified if players actually shoot differently based on their last 5 results, but they don't. Here are the changes in shooting percentages (hot minus cold) for all players:
| BASIC_ZONE | hot | cold | diff |
|:----------------------|------:|-------:|-------:|
| Above the Break 3 | 34.7 | 35 | -0.3 |
| Corner 3 | 38.4 | 38.9 | -0.4 |
| In The Paint (Non-RA) | 41.7 | 41.2 | 0.5 |
| Mid-Range | 39.8 | 40.1 | -0.3 |
| Restricted Area | 62.7 | 60.7 | 2 |
For 3 out of 5 shot types, the hot FG percentages are lower than the cold ones. Combined with the changes in shot selection, I think there's evidence that the league as a whole is scoring less efficiently because of the false belief in the hot hand.
The data says that players are essentially trading Restricted Area (.627 * 2 = 1.25 points per shot) and Corner 3 (.384 * 3 = 1.15 points per shot) attempts for Mid-Ranges (.398 * 2 = .796 points per shot) when they think they've got the hot hand. That's clearly bad! If it happens once a game, that's 38 points a year lost, which might be enough to swing a game or two.
The change in restricted area and in the paint (non-RA) FG% is intriguing, but if the hot hand did exist, wouldn't we see it on 3 point or mid-range shots, rather than restricted area shots? The announcer doesn't say "he's heating up" after a guy has made 3 layups in a row, they say it after 3 longer range shots in a row, right?
Higher volume players
I decided to focus on players with at least 1000 streaks, which leaves 630 players. Collectively, they are responsible for 84% of all shots in the NBA over the last 20 years.
Their FG percentages are, on average, 1% lower when they are hot than when they are cold.
68% of them shoot worse when they're hot than when they're cold, which is a pretty dramatic split.
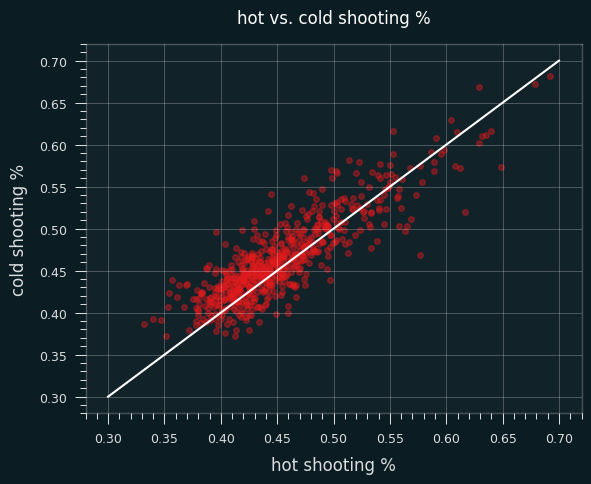
Here's a plot of the difference between hot and cold FG% versus z-score:
Players with negative values on the x axis shoot better when they're cold, and positive values shoot better when they're hot.
Now, there should be some correlation between z-scores and hot/cold shooting tendency. I've shown simulations where a tendency to shoot better cold produces unstreaky results (skewed towards positive z scores), and better hot will produce streaky results (negative z scores). So there should be more dots in the upper left and bottom right quadrants compared to the other diagonal.
But if players behaved by coin flips, we should see roughly the same number of players with positive and negative z scores, and roughly the same number of players who shoot better when they're hot and better when they're cold.
I simulated all 3.5 million shots by these players, using their career average FG% for every shot. So any streakiness or unstreakiness is going to be totally random. As you can see, the data is much less spread out across both the X and Y axis.
Here are the crosstabs from the simulation:
|
better cold |
better hot |
margin |
| positive z |
178 |
135 |
313 |
| negative z |
112 |
210 |
322 |
| margin |
290 |
345 |
|
As promised, the marginal values are pretty close to one another. That's what happens when "better hot" vs. "better cold" and "positive z" vs. "negative z" are determined purely by chance.
Here are the actual crosstabs. The marginal values are much more imbalanced.
|
better cold |
better hot |
margin |
| positive z |
343 |
126 |
469 |
| negative z |
88 |
78 |
166 |
| margin |
431 |
204 |
|
Things to note:
- 68% of the players shoot better when they're cold.
- 74% of the players have a positive z-score.
- Even among players with a negative z score, the majority of them shoot better when they're cold.
- Even among players that shoot better when they're hot, the majority of them still produce results that are less streaky than expected by chance.
That's all super weird!
As always, these are just general trends. There are 78 players in the "better hot" + "negative z" box, and there should be around 210 players. We can't really say which players are the 130 "missing" players, though.
That's all I've got on the hot hand in the NBA for now. I think I understand it a lot better now, and I hope you do, too.



























































